Have you ever wondered why materials fail under repeated stress, even when the stress levels seem manageable? This article dives into the six critical factors affecting the fatigue properties of materials. From the impact of average stress and load forms to the influence of size, surface finish, surface treatment, and environmental conditions, you’ll uncover the complexities that determine material durability. Learn how these elements interplay to predict and enhance the lifespan of components in engineering applications. Discover practical insights to improve fatigue resistance in your next project.
Strain Fatigue (Low Cycle Fatigue): This type of fatigue occurs under high stress levels and with a limited number of cycles. The damage to materials caused by strain fatigue is usually regulated by the acceptable strain value.
Stress Fatigue (High Cycle Fatigue): This type of fatigue occurs under low stress levels and with a high number of cycles. Materials are damaged due to stress fatigue, which is typically regulated by the acceptable stress value.
Secondary Fatigue: This type of fatigue occurs when the stress level drops below a certain value, causing the crack to cease growing.
The fatigue characteristics of materials are represented by the relationship between the applied stress (S) and the number of cycles (N) until failure.
Under a fatigue load, the simplest type of load spectrum is a constant amplitude cyclic stress.
When the stress ratio (R) is equal to -1, the stress-life relationship, obtained from tests under symmetrical constant amplitude cyclic load, represents the basic fatigue performance curve of the material.
The impact of changing the stress ratio (R) on fatigue performance will be discussed later.
As shown in the figure above, the increase of stress ratio R indicates that the average cyclic stress Sm increases. And when the stress amplitude Sa is given, there are:
Sm = (1+R)Sa/(1-R)
In general, when Sa is given, R increases, and the average stress Sm also increases.
The increase of tensile part in cyclic load is unfavorable to the initiation and propagation of fatigue crack, which will reduce the fatigue life.
The general trend of the influence of average stress on the S-N curve is shown in the figure below.
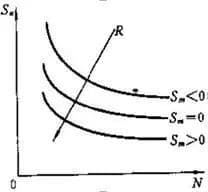
The basic S-N curve is obtained when the average stress, Sm, is equal to zero.
When Sm is greater than zero, meaning the material is subjected to a tensile average stress, the S-N curve shifts downward. This implies that the life of the material under the same stress amplitude decreases, or the fatigue strength decreases under the same life, which has a negative impact on fatigue.
When Sm is less than zero, meaning the material is subjected to a compression average stress, the S-N curve shifts upward. This indicates that the life of the material under the same stress amplitude increases, or the fatigue strength increases under the same life, and the compression average stress has a positive effect on fatigue.
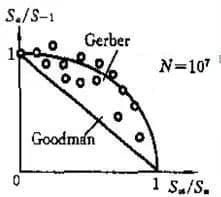
The relationship between cyclic stress amplitude (Sa) and average stress (Sm) is studied for a given life (N), and the results are shown in the accompanying figure.
It is observed that as the average stress (Sm) increases, the corresponding stress amplitude (Sa) decreases. However, it should be noted that the average stress (Sm) can never exceed the ultimate strength (Su) of the material.
The ultimate strength (Su) is defined as the ultimate tensile strength of brittle materials with high strength or the yield strength of ductile materials.
The figure shows the Sa-Sm relationship of metal material N=10^7, which is normalized with the fatigue limit (S-1) and the ultimate strength (Su).
Thus, the Sa-Sm relationship under the condition of equal life can be described as follows:
(Sa/S-1) + (Sm/Sn) = 1
This is the parabolic curve in the figure, known as the Gerber curve, and the data points are primarily located near this curve.
Another representation is the straight line shown in the figure, which is referred to as:
n(Sa/S-1) + (Sm/Sn) = 1
The equation mentioned above is known as the Goodman line and all of the test points are generally above this line.
The straight line form is straightforward and, for a given life, the estimated Sa-Sm relationship is cautious, making it a popular choice in engineering practices.
The fatigue limit of materials exhibits the following trend for various load forms:
S (bending)>S (stretching)>S (twisting)
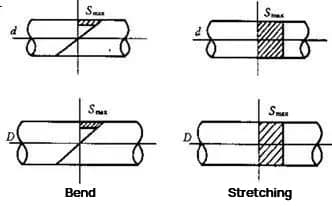
Assuming the same level of applied stress, the volume of the high stress zone in tension and compression is equal to the entire volume of the specimen under test. However, in the case of bending, the high stress zone volume is significantly smaller.
Fatigue failure is primarily determined by two factors: the magnitude of the applied stress (an external cause) and the material’s ability to resist fatigue failure (an internal cause). Failure typically occurs in high stress areas or at material defects.
When the maximum cyclic stress (Smax) in the figure is equal, the large volume of material in the high stress area during tension and compression cycles increases the likelihood of defects and crack initiation. Therefore, under the same stress level, the life of the specimen under tension-compression cyclic load is shorter than under bending.
In other words, for the same service life, the fatigue strength under tension-compression cycles is lower than under bending. The fatigue life decreases even further during torsion, but the volume has little impact.
The differences in fatigue life under different stress states can be explained by different failure criteria, but will not be further discussed here.
The impact of different specimen sizes on fatigue performance can also be attributed to the varying volume of the high stress zone.
When the stress level remains constant, a larger specimen size results in a larger volume of material in the high stress area.
Fatigue occurs at the weakest point in the material within the high stress area. The larger the volume, the higher the probability of defects or weak points.
Therefore, the fatigue resistance of large-sized components is lower than that of small-sized specimens. This means that, for a given life N, the fatigue strength of large-sized components decreases. Additionally, under a given stress level, the fatigue life of large-sized components also decreases.
It is clear from the concept of fatigue locality that a rough surface on the specimen leads to an increase in local stress concentration, which shortens the crack initiation life.
The basic S-N curve of the material is determined by measuring the standard specimen with a good finish, which is achieved through fine grinding.
As a general rule, fatigue cracks always originate from the surface. To enhance the fatigue performance, various methods are frequently employed in addition to improving the surface finish. These methods aim to introduce compressive residual stress on the high stress surface of the component, with the goal of increasing fatigue life.
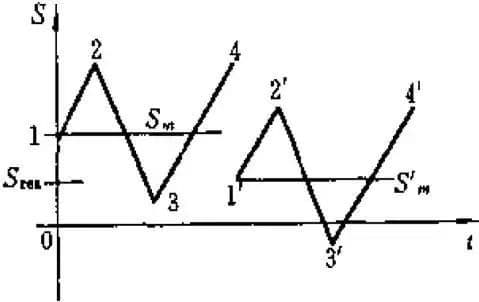
If the cyclic stress is as shown in the sequence 1-2-3-4, and the average stress is represented by Sm, the addition of a compression residual stress Sres will result in a new stress level of 1′-2′-3′-4′, which is a superposition of the original stress sequence and -Sres. This leads to a reduction in the average stress to S’m, resulting in improved fatigue performance.
Common methods to enhance the fatigue life of components include surface shot peening, cold extrusion of parts, and the introduction of residual compressive stress on their surface.
The strength of the material has a direct impact on its fatigue performance. Higher material strength leads to a lower cyclic stress level and, therefore, a longer service life and improved life extension effects.
Shot peening is especially effective in areas with stress gradients or notch stress concentrations.
Surface nitriding or carburizing treatments can improve the strength of the material surface and induce compressive residual stress, both of which contribute to improved fatigue performance.
Test results indicate that nitriding or carburizing treatments can double the fatigue limit of steel. This effect is even more pronounced in specimens with notches.
The S-N curve of materials is typically obtained under room temperature and atmospheric conditions.
Fatigue in corrosive environments such as seawater, acids, and alkalis is referred to as corrosion fatigue.
The presence of corrosive media has a detrimental effect on fatigue.
Corrosion fatigue is a complex process that involves both mechanical and chemical actions and its failure mechanism is complex.
There are several factors that influence corrosion fatigue, and the general trend is as follows:
(1) The effect of load cycle frequency is significant. In non-corrosive environments, frequency has little effect on the S-N curve of materials in a relatively wide frequency range (such as 200Hz). However, in corrosive environments, as the frequency decreases, the time experienced by the same cycle number increases, providing sufficient time for corrosion to have a significant impact on the decline of fatigue performance.
(2) Semi-immersion in corrosive media (such as seawater) is more unfavorable than complete immersion.
(3) Corrosion-resistant steels with good corrosion fatigue resistance perform better than ordinary carbon steels, which see a significant decrease in their fatigue limit, or even its complete disappearance, in corrosive environments.
(4) The fatigue limit of metal materials generally increases with decreasing temperature. However, with decreasing temperature, the material’s fracture toughness also decreases, leading to low temperature brittleness. Once cracks occur, instability fracture is more likely to occur. High temperatures reduce the strength of materials, can cause creep, and are unfavorable to fatigue. It should also be noted that the residual compressive stress introduced to improve fatigue performance will also disappear with increasing temperature.
As the founder of MachineMFG, I have dedicated over a decade of my career to the metalworking industry. My extensive experience has allowed me to become an expert in the fields of sheet metal fabrication, machining, mechanical engineering, and machine tools for metals. I am constantly thinking, reading, and writing about these subjects, constantly striving to stay at the forefront of my field. Let my knowledge and expertise be an asset to your business.
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO