Typically, the S-N curves obtained from manual testing are based on the results from standard specimens without notches. However, the actual parts used in real-world applications may have different shapes, sizes, surface conditions, working environments, and load characteristics, all of which can significantly impact the fatigue strength of the parts.
The factors that affect fatigue strength can be grouped into three categories: mechanics, metallurgy, and environment. These factors are interdependent, making it challenging to comprehensively evaluate their impact on fatigue strength design and fatigue life prediction.
Mechanical factors are primarily influenced by stress concentration and average stress. Metallurgical factors are related to the quality of the material, such as its purity and strength. Environmental factors, on the other hand, include the presence of corrosive substances and high temperatures.
For railway vehicle parts, which mostly operate in normal atmospheric conditions at normal temperatures, the main focus should be on mechanical and metallurgical factors, such as the influence of notch shape, size, surface condition, and average stress.
Specific information on the influence of these factors on the fatigue limit can be found in relevant manuals and materials through the use of empirical formulas.
This article aims to discuss the important laws and phenomena that need to be understood in fatigue strength design and fatigue life prediction, as well as the precautions that must or should be taken into consideration.
1. Notch shape effect
Parts or components often have notches, such as shoulder steps, bolt holes, oil holes, keyways, etc. The defining characteristic of these notches is that the cross-sectional area of the parts experiences a sudden change at the notch, causing the stress at the root of the notch to increase significantly. This increase in stress is referred to as stress concentration.
Stress concentration at the notch is the primary factor responsible for reducing the fatigue strength of components. The stress concentration causes the actual stress at the root of the notch to be much higher than the nominal stress, leading to the formation of fatigue cracks and eventually resulting in the failure or damage of the part.
The extent of stress concentration is described by the stress concentration factor (also known as the theoretical stress concentration factor) Kt, which is expressed as follows:
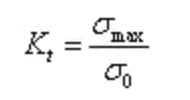
Here, σmax represents the maximum stress, and σ0 represents the average stress calculated by dividing the load by the net cross-sectional area at the notch, also referred to as the nominal stress.
Within a certain range, the smaller the curvature radius ρ at the notch root, the greater the stress concentration and the greater the reduction in fatigue strength. However, for plastic materials like low and medium carbon steel, as the curvature radius at the notch root becomes smaller and approaches a few millimeters, the reduction in fatigue strength becomes smaller or even ceases to reduce.
In this case, the stress concentration factor is no longer an accurate reflection of the impact of the notch on fatigue strength. To more accurately reflect the true reduction in fatigue strength, the fatigue notch factor Kf (previously known as the effective stress concentration factor) is often used.
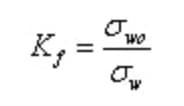
Here, σw0 and σw represent the fatigue limits of smooth specimens without notches and specimens with notches, respectively.
The following figure illustrates the relationship between the stress concentration factor Kt and the fatigue notch factor Kf for steel.
As shown in the figure, for low and medium carbon steel, when the stress concentration factor is less than 2 to 2.5, Kt and Kf are generally similar. However, when this value is exceeded, the increase in Kf slows down significantly.
For high-carbon steel with a high strength ratio, Kf increases linearly with Kt over a long range.
It can be concluded that the fatigue strength of high-strength steel is highly sensitive to the presence of notches, whereas the fatigue strength of low and medium-strength steel is less sensitive to notches.
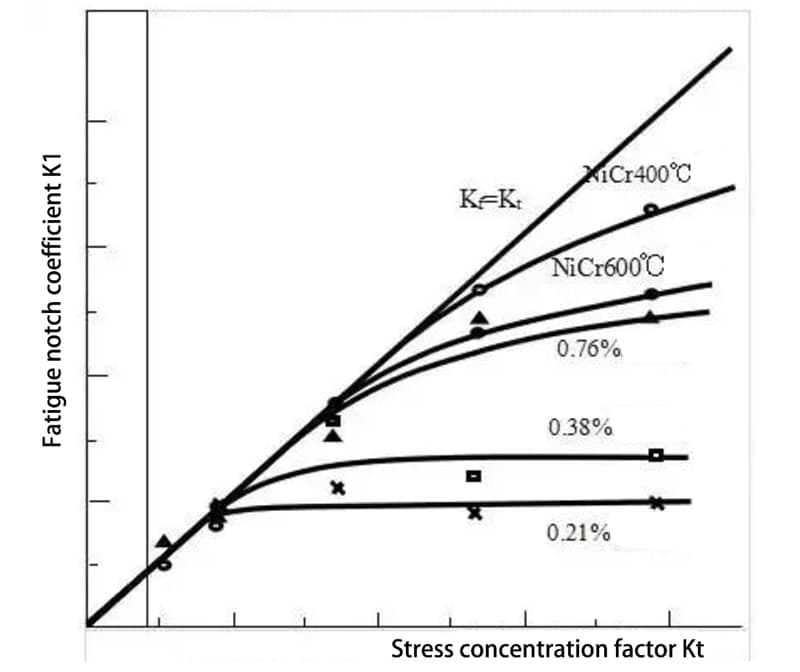
Generally, Kf is less than Kt, but in the case of sharp notches in high-carbon steel, Kt may be greater than Kf. This can also occur in bolt parts, where Kt can reach 4 and Kf can be 8 to 10. This is due to the uneven distribution of load among the threads, with several loads concentrated on one thread.
For smooth materials, surface heat treatments such as surface quenching, carburizing, and nitriding can effectively improve their fatigue strength. However, these methods may be ineffective or even reduce the fatigue strength of notched materials. This is because surface strength is improved through heat treatment, but the sensitivity to notches also increases.
The following figure illustrates the change in the fatigue strength of notched high-strength steel and low-strength steel with good plasticity as the stress concentration increases. In the range of smaller stress concentration Kt, the fatigue strength of high-strength steel is significantly higher than that of low-strength steel. However, as the stress concentration factor increases, the fatigue strength of high-strength steel decreases more rapidly than that of low-strength steel, resulting in the fatigue strength of high-strength steel being nearly equal to that of low-strength steel.
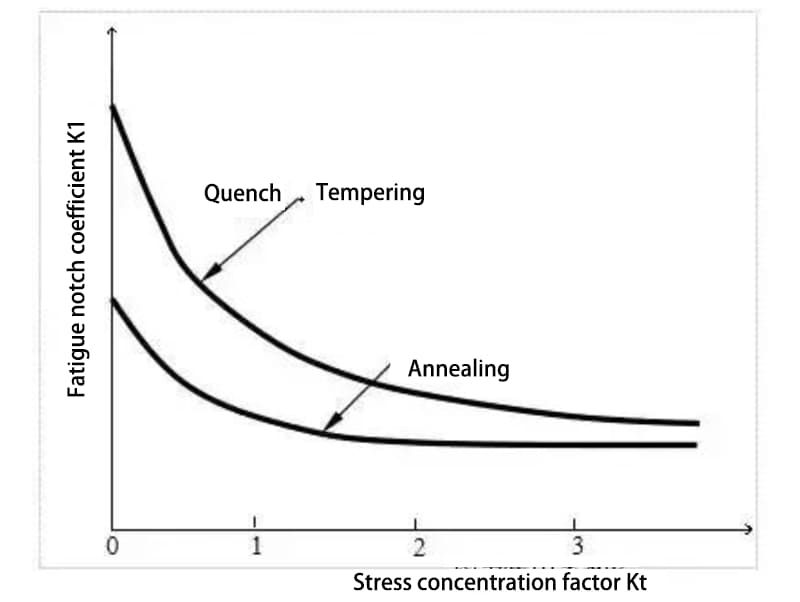
For welded components, the fatigue strength is often significantly reduced due to the combination of the heat affected zone being located near the structural notch and the presence of welding defects and residual tensile stress. This reduction can be several times greater than normal or even more than ten times.
The fatigue notch coefficient can also be impacted by the size of the parts. As a general rule, for the same notch, the fatigue notch coefficient increases with an increase in size.
To improve the fatigue life of notched materials or components with notches, it is most effective to undertake structural design and process selection that reduces or improves stress concentration.
However, a rough surface and large size can reduce the fatigue strength of components.
2. Size effect of parts
The diameter of the specimen used for fatigue testing is typically between 5-10mm, which is much smaller than the actual size of parts.
For components subjected to bending and torsion loads, the fatigue strength decreases as the size increases. However, for axial tension and compression loads, the size has a minimal effect.
The size’s influence on the fatigue limit is represented by the size influence coefficient (ε).
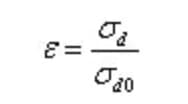
Here, σd and σd0 represent the fatigue limits of smooth specimens of any size and the standard size, respectively.
The size effect on high strength steel is greater than that of low strength steel, and the size effect is more pronounced for parts with rough surfaces.
The size effect is primarily due to the impact of the material’s structure state and stress gradient on the fatigue strength of larger components.
As the size of the material increases, it becomes more challenging to control the manufacturing process, and the material structure becomes less uniform and compact, with more metallurgical defects and a larger surface area that increases the likelihood of these defects.
This results in a higher risk of fatigue and cracks on the surface of large specimens. The local stress concentration caused by metallurgical defects leads to the formation of fatigue cracks.
Regarding the influence of stress gradient, when subjected to bending, torsion, and other loads, the larger the size of the component, the smaller the gradient of working stress, the higher the average stress per unit area, and the easier it is for fatigue cracks to form.
3. Effect of surface condition
The surface conditions affect various factors such as surface roughness, surface stress state, degree of surface plastic deformation, surface defects, and others.
In the testing process, the standard sample with a polished surface is used, however, the actual parts often have machined, forged, or cast surfaces.
Machining can result in plastic work hardening on the part’s surface.
Cutting often leaves residual compressive stress on the surface, which improves the fatigue strength but only to a limited extent.
Grinding, on the other hand, can cause residual tensile stress, which is detrimental to the fatigue strength.
Furthermore, the micro-scale roughness of machined surfaces can lead to stress concentration and decrease fatigue strength.
The combined effect of these factors results in a lower fatigue strength compared to the standard sample.
Forged or cast surfaces typically have higher roughness and surface work hardening layers, as well as residual compressive stresses, leading to a significant decrease in fatigue strength.
In conclusion, the rougher the surface processing method, the greater its impact on reducing fatigue strength.
The effect of surface processing conditions on fatigue strength is represented by the surface processing coefficient (β).
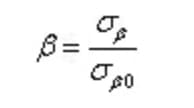
Here, σβ represents the fatigue limit of a standard smooth sample in a certain surface state, σβ0 represents the fatigue limit of a polished standard smooth sample, and “abroad” refers to the standard smooth sample with a polished surface.
From a metallurgical perspective, rough machining has a significant impact on the fatigue strength of high-strength materials, so high-strength steel may not enhance fatigue strength in rough machining states. This is mainly due to the high notch sensitivity of high-strength materials to rough surfaces and the minimal work-hardening effect of machining on the surface of high-strength steel.
Little research has been done on the impact of surface defects, such as surface decarburization, surface bump marks, and scratches, on fatigue strength. However, surface defects caused by accidental reasons can have a significant impact on fatigue strength. Therefore, sufficient attention should be paid to these issues in the design and especially in the manufacturing process.
For smooth materials, surface heat treatment and other surface modification methods can improve fatigue strength. However, for materials with notches, such as actual parts, these methods have little effect and may even have an adverse effect. As a result, shot peening and rolling are often used to generate work hardening and residual compressive stress on the surface, thereby improving the fatigue strength of components.
However, these two methods generally do not significantly improve the fatigue strength of parts with holes. The latest research shows that using a simple metal die to chamfer a small amount of the edge of the hole can significantly improve fatigue strength and even eliminate the impact of the notch, reducing the fatigue limit.
In the past, it was commonly believed that the main reason for the improvement in fatigue strength from surface plastic processing methods was due to the residual compressive stress generated on the surface offsetting some of the working stress.
However, the compressive concentrated stress produced by the residual compressive stress at the notch offset the adverse effect of the notch. The plastic deformation strengthens the weak areas near the notch, making the structure more uniform and improving overall strength, which in turn improves the stress level that produces fatigue cracks.
Additionally, the residual compressive stress makes fatigue cracks stop growing and become stay cracks.
4. Effect of average stress
As previously stated, the primary cause of fatigue failure is dynamic stress, but the static stress component, or average stress, also has some impact on the fatigue limit. In a specific range of static stress, an increase in compressive static stress will raise the fatigue limit, whereas an increase in tensile static stress will lower it.
It is widely accepted that residual stress has a similar effect on the fatigue limit as average stress. For a given material, a fatigue limit diagram can be plotted based on its fatigue limit results under varying average stresses or stress ratios (R).
The diagram below features a dimensionless quantity, the ratio of average stress (σm) or residual stress, to the strength limit (σb), on the x-axis, and the ratio of stress amplitude (σa) to the symmetrical cyclic fatigue limit (σ-1), on the y-axis.

The figure depicts that most test data points lie between straight lines and curves. The straight line is referred to as the Goodman line, while the curve is known as the Gerber parabola. The Soderberg line is obtained by substituting the strength limit (σb) with the yield limit (σs). Similarly, the Morrow line is derived by replacing σb with the true fracture stress (σf).
Goodman line:
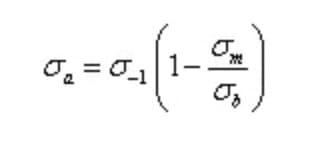
Gerber line:

Soderberg line:

Morrow line:

The Goodman line is a conservative and straightforward approach for ductile metals, making it a widely used method in fatigue design. Another frequently used method is the Ideal Improved Goodman Diagram.
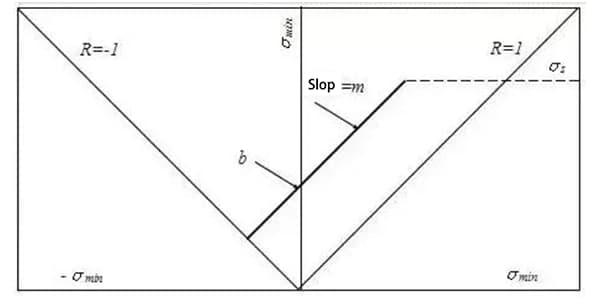
The following figure illustrates the Ideal Improved Goodman Diagram of an I-shaped steel butt beam under bending fatigue load. The x-axis represents the minimum stress (σmin), the y-axis represents the maximum stress (σmax), and the linear equation is as follows:

Where, m is the slope of Goodman line, b is the intercept of the line on the y-axis, and it is the fatigue limit of pulsation cycle when the minimum stress is equal to zero.
When the fatigue limit is expressed by the maximum stress, namely σ w= σ Max, considering the stress ratio R= σ max/ σ Min.
Morrow line includes:

The fatigue limit at a given stress ratio (R) can be calculated using the above formula. However, the actual structure of a vehicle is much more complex than the test conditions under which the S-N curve was obtained, such as the type of welding and stress concentrations.
The American AAR standard provides valuable guidelines for the fatigue strength of various welding structures, and thus, the values of “b” and “m” in actual calculations are taken from the AAR standard.
Test results indicate that the impact of static load components on the stress concentration coefficient, dimension coefficient, and surface coefficient is minor and can be disregarded.


