1. Materiales experimentales 1.1 Parámetros de rendimiento del material En el experimento se estudió el acero de alta resistencia DP590, cuya composición química se muestra en la Tabla 1, y los parámetros de rendimiento se muestran en la Tabla 2. Tabla 1 Composición química del material (fracción másica) Grado del material C Si Mn P S Al Ti DP590 0,078 0,03 1,76 0,01 0,004 ≥ 0,020 [...]
El experimento estudió el acero de alta resistencia DP590, cuya composición química se muestra en la Tabla 1, y los parámetros de rendimiento se muestran en la Tabla 2.
Tabla 1 Composición química del material (fracción másica)
| Calidad del material | C | Si | Mn | P | S | Al | Ti |
| DP590 | 0.078 | 0.03 | 1.76 | 0.01 | 0.004 | ≥ 0.020 | – |
Cuadro 2 Rendimiento de los materiales Parámetros
| Parámetro | Valor |
| Exponente de endurecimiento del trabajo n | | 0.13 |
| Relación de Poisson μ | 0.33 |
| Módulo elástico E/MPa | 199 000 |
| Exponente de endurecimiento K | 1 003 |
| Límite elástico/MPa | 318 |
| Resistencia a la tracción/MPa | 626 |
| Relación rendimiento/tensión/% | 50 |
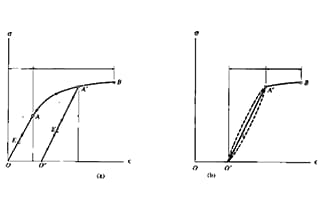
El ensayo de tracción se llevó a cabo de acuerdo con la norma de ensayo GB/T 228.1-2010, y la curva tensión-deformación real obtenida a partir de los datos del ensayo se muestra en la Figura 1.
Basándose en el caso estándar internacional NUMISHEET2011 y en el tamaño de las piezas de viga utilizadas habitualmente en la producción real, se determina que el tamaño de la placa utilizada para la pieza en forma de U es de 100 mm × 360 mm × 1,2 mm.
La estructura bidimensional ensamblada se muestra en la Figura 2, y las dimensiones geométricas de las piezas del molde se muestran en la Tabla 3. El modelo se creó en el software UG NX de acuerdo con el dibujo, y la estructura explosiva se ensambló como se muestra en la Figura 3.
A continuación, se importó en Dynaform para el mallado y la parametrización básica del proceso, como se muestra en la figura 4.
Tabla 3 Dimensiones geométricas de las piezas del molde
| Parámetro | Dimensiones/mm |
| W1 | 80 |
| W2 | 84 |
| W3 | 135 |
| W4 | 135.5 |
| R1 | 5.0 |
| R2 | 7.0 |
| G1 | 1.2 |
| accidente cerebrovascular | 70 |
Durante el proceso de estampación, la chapa sufrirá grandes deformaciones elásticas.
En la fase final de la estampación, la descarga de la carga hará que se libere la energía elástica generada anteriormente, provocando la tensión interna para recombinarse, cambiando así la forma de la pieza. Esto da lugar al defecto de springback de la chapa.
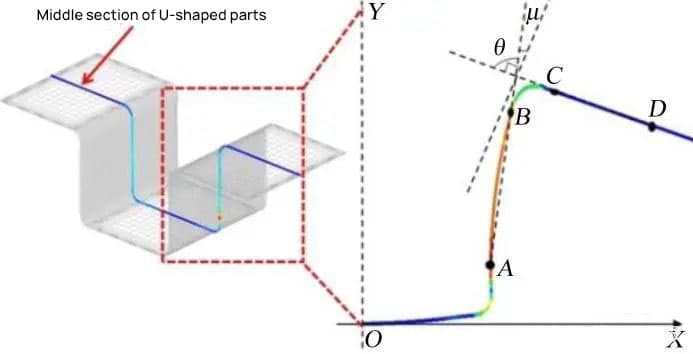
Ahora, se selecciona la sección central de la pieza en forma de U para medir el springback situación, como se muestra en la Figura 5.
La amplitud del springback se caracteriza por el ángulo complementario μ del ángulo θ entre las superficies AB y CD. Cuanto mayor sea el ángulo μ, mayor será la amplitud del springback.
Los factores que afectan al springback de las piezas estampadas son principalmente estructura del moldeLa forma y las propiedades mecánicas de la chapa, así como los parámetros del proceso de estampación.
En vista de la estructura y el estampado características del proceso de la pieza en forma de U, se seleccionaron cuatro factores principales que incluían la fuerza de rebordeado, el coeficiente de fricción, el espesor de la chapa y el radio de la esquina del punzón para explorar la influencia de los diferentes factores en la variación del ángulo de springback.
Bajo las condiciones de uso de acero de alta resistencia DP590 con un espesor de 1,2 mm y un coeficiente de fricción de 0,125, y una separación (G1) de 1,2 mm entre el punzón y la matriz, se estudió la influencia de la fuerza de rebordeado en el springback realizando simulaciones de conformado y springback con fuerzas de rebordeado que oscilaban entre 10 kN y 120 kN.
La influencia de la fuerza de rebordeado en el ángulo de springback obtenido mediante simulación se muestra en la Tabla 4 y en la Figura 6.
Tabla 4 Relación entre la fuerza de rebordeado y el springback.
| Fuerza de rebordeado/kN | Ángulo de retroceso（°） |
| 10 | 8.126 |
| 20 | 8.902 |
| 40 | 7.734 |
| 60 | 6.660 |
| 80 | 5.572 |
| 100 | 4.226 |
| 120 | 3.686 |
Como se muestra en la figura 6, el ángulo de springback de la pieza aumenta inicialmente y luego disminuye. De la Tabla 4 se desprende que cuando la fuerza de rebordeado varía de 10 kN a 120 kN, el cambio máximo en el ángulo de springback es de 5,216°, lo que indica que el control de la fuerza de rebordeado tiene un efecto más evidente en el ángulo de springback.
La razón de este fenómeno es la siguiente: cuando la fuerza de rebordeado es pequeña, la pieza se forma principalmente por flexión. La chapa produce tensiones de flexión bajo la acción del punzón, y las tensiones de flexión se liberan tras la descarga del punzón, lo que provoca un aumento del springback.
Cuando la fuerza de rebordeado aumenta hasta cierto punto, la deformación plástica del material aumenta, haciendo que la cantidad de deformación elástica liberada por la chapa disminuya y, por lo tanto, el springback también disminuye.
En las condiciones de utilización de una fuerza de rebordeado de 40 kN y una separación de 1,2 mm entre el punzón y la matriz, se estudió la influencia del coeficiente de fricción en el springback realizando simulaciones de conformado y springback con coeficientes de fricción que oscilaban entre 0,025 y 0,275.
La influencia del coeficiente de fricción sobre el ángulo de springback obtenido mediante simulación se muestra en la Tabla 5 y en la Figura 7.
Tabla 5 Relación entre el coeficiente de fricción y el springback.
| Coeficiente de fricción | Ángulo de retroceso（°） |
| 0.025 | 8.126 |
| 0.075 | 8.902 |
| 0.125 | 7.734 |
| 0.175 | 6.660 |
| 0.225 | 5.572 |
| 0.275 | 4.226 |
La tabla 5 muestra que cuando el coeficiente de fricción varía de 0,025 a 0,275, el cambio máximo en el ángulo de springback es de 4,676°, lo que indica que el control del coeficiente de fricción tiene un efecto más evidente en el ángulo de springback.
Como se muestra en la figura 7, el ángulo de springback de la chapa aumenta primero y disminuye después con el aumento del coeficiente de fricción.
La razón del fenómeno anterior es: inicialmente, debido a que el coeficiente de fricción es pequeño, la resistencia a la fricción del material es pequeña, y el proceso de conformado de la chapa es principalmente de flexión, lo que da lugar a una gran cantidad de springback.
A medida que aumenta gradualmente el coeficiente de fricción, también aumenta la resistencia a la fricción del material. Cuando la resistencia a la fricción es lo suficientemente grande, el borde de la chapa es difícil de mover, y el proceso de conformado de la pieza es principalmente deformación plástica.
Una vez descargado el punzón, la chapa liberará menos energía potencial elástica y, por tanto, el springback de la chapa disminuirá.
En las condiciones de uso de una fuerza de rebordeado de 40 kN, una separación de 1,2 mm entre el punzón y la matriz, un coeficiente de fricción de 0,125 y un radio de punzón de R5 mm, se estudió la influencia del espesor de la chapa en el springback realizando simulaciones de conformado y springback con espesores de chapa comprendidos entre 1,0 mm y 1,8 mm.
La influencia del espesor de la chapa en el ángulo de springback obtenido mediante simulación se muestra en la Tabla 6 y en la Figura 8.
Tabla 6 Relación entre el espesor de la chapa y el springback.
| Espesor de chapa/mm | Ángulo de retroceso（°） |
| 1 | 10.541 |
| 1.2 | 7.734 |
| 1.4 | 5.448 |
| 1.6 | 3.814 |
| 1.8 | 2.030 |
Como se muestra en la Tabla 6, cuando el espesor de la chapa varía de 1,0 mm a 1,8 mm, el cambio máximo en el ángulo de springback es de hasta 8,511°, que es el mayor entre los cuatro factores seleccionados, lo que indica que el control del espesor de la chapa tiene un efecto relativamente obvio en el ángulo de springback.
Como se muestra en la figura 8, el ángulo de springback de la chapa disminuye con el aumento del espesor de la chapa.
Esto se debe principalmente a que, bajo la condición de radio de punzón constante, cuanto mayor sea el espesor de la chapa, menor será la relación de radio de curvatura al espesor de la chapa, lo que se traduce en una menor deformación por flexión de la chapa y una menor proporción de deformación elástica en la deformación total.
Por lo tanto, cuando el punzón se descarga, el springback de la chapa disminuye.
Bajo las condiciones de uso de una fuerza de rebordeado de 40 kN y un coeficiente de fricción de 0,125, se estudió la influencia del radio de la esquina del punzón en el springback realizando simulaciones de conformado y springback con radios de esquina del punzón que oscilaban entre R3 mm y R7 mm.
La influencia del radio de la esquina del punzón en el ángulo de springback obtenido mediante simulación se muestra en la Tabla 7 y en la Figura 9.
Tabla 7 Relación entre el radio de la esquina del punzón y el springback.
| Radio del filete del punzón/mm | Ángulo de retroceso（°） |
| 3 | 6.388 |
| 4 | 6.982 |
| 5 | 7.734 |
| 6 | 8.153 |
| 7 | 8.553 |
Según las observaciones de la Tabla 7 y la Figura 9, el aumento del radio del filete del punzón de 3 mm a 7 mm produce un aumento del ángulo de springback de 6,388° a 8,553°.
Este comportamiento se atribuye al aumento del área de contacto entre el filete del punzón y la chapa, lo que aumenta posteriormente la deformación por flexión, provocando un mayor efecto de springback.
No obstante, de la Tabla 7 se desprende que el cambio en el valor máximo del springback de 3 mm a 7 mm en el radio del filete del punzón es de sólo 2,165°, que es el efecto más pequeño entre los cuatro factores seleccionados.
Esto implica una influencia mínima del radio del filete del punzón sobre el ángulo de springback.
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
AR 
DE 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO