Streckgrenze: Sie ist die Ertragsgrenze einer Metallmaterial wenn es nachgibt, d. h. die Spannung, die einer leichten plastischen Verformung widersteht.
Für metallische Werkstoffe ohne offensichtliches Fließen, wird der Spannungswert, der eine Restverformung von 0,2% hervorruft, als Fließgrenze angegeben und als bedingte Fließgrenze oder Streckgrenze bezeichnet.
Äußere Kräfte, die diesen Grenzwert überschreiten, führen zu einem dauerhaften Versagen des Bauteils und können nicht wiederhergestellt werden. Die Streckgrenze von kohlenstoffarmem Stahl beträgt beispielsweise 207 MPa.
Wenn äußere Kräfte einwirken, die diesen Grenzwert überschreiten, wird das Bauteil dauerhaft verformt. Liegt der Grenzwert darunter, kehrt das Bauteil in seine ursprüngliche Form zurück.
Die traditionelle Festigkeitsberechnungsmethode betrachtet die Streckgrenze als Standard für plastische Werkstoffe, mit der zulässigen Spannung [σ]=σys/n, wobei der Sicherheitsfaktor n je nach Situation zwischen 1,1 und 2 oder mehr liegen kann.
Für spröde Werkstoffe wird die Zugfestigkeit als Maßstab genommen, wobei die zulässige Spannung [σ]=σb/n und der Sicherheitsfaktor n im Allgemeinen mit 6 angenommen wird.
Es ist zu beachten, dass die traditionelle Festigkeitsberechnungsmethode unweigerlich zu einem einseitigen Streben nach einer hohen Streckgrenze des Werkstoffs führt, dass aber mit zunehmender Streckgrenze des Werkstoffs die Bruchfestigkeit abnimmt und das Bruchrisiko steigt.
Die Streckgrenze hat nicht nur eine unmittelbare praktische Bedeutung, sondern dient auch als grobes Maß für das mechanische Verhalten und die Prozessleistung eines Werkstoffs in der Technik.
Je höher die Streckgrenze des Werkstoffs ist, desto empfindlicher ist er gegen Spannungskorrosion und Wasserstoffsprödbruch; sinkt die Streckgrenze, so ist die Kaltumformung Leistung und Schweißleistung verbessern sich, und so weiter.
Daher ist die Streckgrenze ein unverzichtbarer wichtiger Index für die Leistungsfähigkeit von Materialien.
Stress
Wenn sich ein Objekt aufgrund äußerer Faktoren (Kräfte, Feuchtigkeit, Temperaturschwankungen usw.) verformt, wirken innere Kräfte zwischen den verschiedenen Teilen des Objekts. Die innere Kraft pro Flächeneinheit wird als Spannung bezeichnet.
Die senkrecht zum Querschnitt verlaufenden Spannungen werden als Normalspannungen oder Axialspannungen bezeichnet, die tangential zum Querschnitt verlaufenden Spannungen als Scherspannungen oder Schnittspannungen.
Stämme
Unter Dehnung versteht man die relative Verformung eines Objekts unter Einwirkung äußerer Kräfte und ungleichmäßiger Temperaturfelder sowie anderer Faktoren.
Nach dem Hooke'schen Gesetz stehen Spannung und Dehnung innerhalb eines bestimmten proportionalen Grenzbereichs in einem linear proportionalen Verhältnis.
Die entsprechende maximale Spannung wird als Proportionalitätsgrenze bezeichnet.
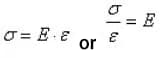
Das Verhältnis von Spannung zu Dehnung, bezeichnet mit E, wird als Elastizitätsmodul oder Youngscher Modul bezeichnet, und verschiedene Materialien haben einen festen Youngschen Modul.
Obwohl die Spannung nicht direkt gemessen werden kann, lässt sie sich durch Messung der durch äußere Kräfte verursachten Dehnung berechnen.
Zusätzliche Informationen
Das Hooke'sche Gesetz ist ein grundlegendes Gesetz in der Theorie der mechanischen Elastizität, das besagt, dass feste Materialien ein lineares Verhältnis zwischen Spannung und Dehnung (Verformungseinheit) aufweisen, wenn sie einer Belastung ausgesetzt sind.
Materialien, die das Hooke'sche Gesetz erfüllen, werden als linear elastische oder Hooke'sche Materialien bezeichnet.
Der Ausdruck des Hooke'schen Gesetzes ist F=k-x oder ΔF=k-Δx, wobei k eine Konstante ist, der Steifigkeitskoeffizient des Objekts.
Im Internationalen Einheitensystem ist die Einheit von F Newton, die Einheit von x ist Meter und ist eine Verformungsgröße (elastische Verformung), und die Einheit von k ist Newton/Meter.
Der Steifigkeitskoeffizient ist numerisch gleich der Federkraft, wenn die Feder um eine Längeneinheit gedehnt (oder verkürzt) wird.
Welche Arten von Stress gibt es?
Normale Spannung: Die Spannungskomponente senkrecht zum Querschnitt wird als Normalspannung (oder Axialspannung) bezeichnet und mit σ angegeben.
Die Normalspannung stellt die Dehnung und Stauchung zwischen benachbarten Querschnitten innerhalb des Bauteils dar.
Normale Dehnung: Die normale Dehnung an einem Punkt ist die Dehnung entlang der Richtung der Normalkraft aufgrund der auf den Querschnitt in dieser Richtung verteilten Normalspannung.
Scherspannung: Die Spannungskomponente, die tangential zum Querschnitt verläuft, wird als Scherspannung oder Scherkraft bezeichnet und mit τ bezeichnet. Die Scherspannung stellt die Gleitwirkung zwischen zwei Teilen dar.
Scherdehnung: Die Scherdehnung an einem Punkt ist die Änderung des Winkels zwischen zwei senkrechten Richtungen aufgrund der auf den Querschnitt verteilten Scherspannung. Sie wird auch als Scherverformung bezeichnet.
Welche Arten von Belastungen gibt es?
Es gibt hauptsächlich zwei Arten von Dehnungen: lineare Dehnungen und Winkeldehnungen. Die lineare Dehnung, die auch als normale Dehnung bezeichnet wird, ist das Verhältnis zwischen der (bei Dehnung positiven) Zunahme der Länge eines kleinen Liniensegments in einer bestimmten Richtung und seiner ursprünglichen Länge.
Die Winkeldehnung, auch bekannt als Scherdehnung oder Scherverformung, ist die Änderung des Winkels (positiv, wenn er kleiner wird) zwischen zwei senkrecht zueinander stehenden Liniensegmenten aufgrund der Scherspannung. Sie wird in Radiant ausgedrückt.
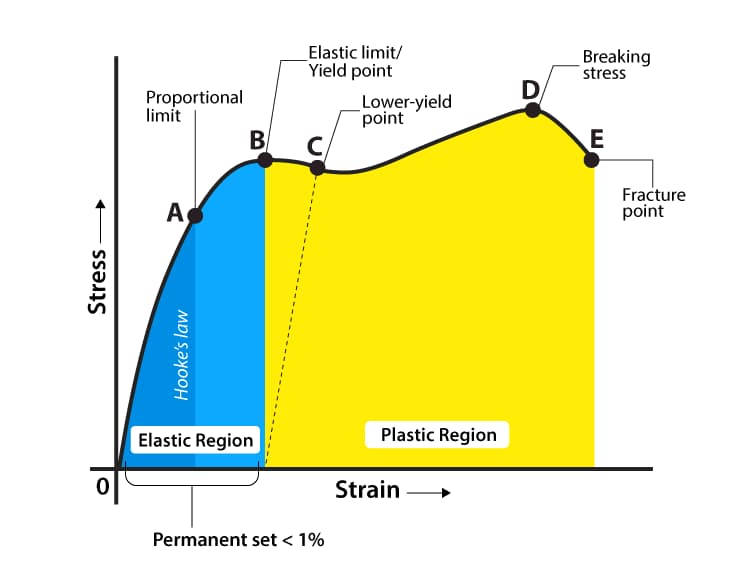
Das Diagramm der Spannungs-/Dehnungskurve (σ-ε) ist in Abbildung 3 dargestellt.
Anstelle der Axiallast F wird die Nennspannung σ = F / A0 und anstelle der Dehnung Δl die technische Dehnung ε = Δl / l0 verwendet.
Die Spannungs-Dehnungs-Kurve hat noch vier Stufen. Die Bedeutungen der einzelnen charakteristischen Punkte sind:
Stufe o bis a:
In der Anfangsphase der Dehnung (oder Kompression) stehen Spannung σ und Dehnung ε bis zum Punkt a in einem linearen Verhältnis.
An diesem Punkt wird der Spannungswert, der dem Punkt a entspricht, als Proportionalitätsgrenze bezeichnet und durch σp dargestellt.
Es ist die maximale Grenze, bei der Spannung und Dehnung proportional sind.
Wenn σ≤σp ist, gilt σ =Eε, auch bekannt als Hooke'sches Gesetz, das besagt, dass Spannung und Dehnung proportional sind.
Daher ist E =σ / ε = tanα, wobei E als Elastizitätsmodul oder Elastizitätsmodul bezeichnet wird und die Einheiten dieselben sind wie σ. Wenn die Spannung die Proportionalitätsgrenze überschreitet, um den Punkt b zu erreichen, weicht die Beziehung σ-ε von einer Geraden ab.
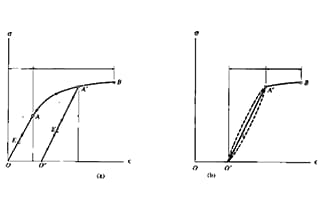
Wenn die Spannung an diesem Punkt auf Null entlastet wird, verschwindet auch die Dehnung (sobald die Spannung den Punkt b überschreitet, kann ein Teil der Dehnung nach der Entlastung nicht mehr beseitigt werden).
Die im Punkt b definierte Spannung wird als Elastizitätsgrenze σe bezeichnet. σe ist der Grenzwert für die ausschließlich elastische Verformung des Materials.
Stufe b bis c:
Nachdem die Spannung die Elastizitätsgrenze überschritten hat, kommt es zu einem Phänomen, bei dem die Spannung nur sehr wenig oder gar nicht zunimmt, während die Dehnung schnell ansteigt.
Dieses Phänomen wird als Fließen bezeichnet. Der Punkt, an dem das Fließen beginnt, entspricht der Streckgrenze σs, die auch als Streckgrenze bezeichnet wird.
Im Stadium des Nachgebens ändert sich die Spannung nicht, während die Dehnung weiter zunimmt. Das Material scheint seine Fähigkeit verloren zu haben, der Verformung zu widerstehen, was zu einer erheblichen plastischen Verformung führt (wenn es zu diesem Zeitpunkt entlastet wird, verschwindet die Dehnung nicht vollständig, und es bleibt eine Restverformung).
Daher ist σs eine wichtige Kennzahl zur Messung der Materialfestigkeit.
Wenn eine Probe aus kohlenstoffarmem Stahl beim Polieren der Oberfläche nachgibt, weist die Oberfläche Schlieren in einem Winkel von 45° zur Achse auf, die auf das relative Gleiten des inneren Kristallgitters zurückzuführen sind und als Gleitlinien bezeichnet werden.
Stufe c bis e:
Nach dem Überschreiten der Streckgrenze muss die Probe weiter belastet werden, wenn sie sich weiter verformen soll; das Material scheint sich verfestigt zu haben, und die c-e-Phase ist die Verfestigungsphase.
Der höchste Punkt (Punkt e) in der Phase der Dehnungsverstärkung entspricht der Festigkeitsgrenze σb. Er stellt die maximale Spannung dar, der das Material standhalten kann.
Stufe e bis f:
Nach dem Überschreiten des Punktes e, d. h. nachdem die Spannung die Festigkeitsgrenze erreicht hat, erfährt die Probe eine starke lokale Kontraktion, die als Einschnürung bezeichnet wird.
Dann entstehen Risse im Inneren der Probe, die Nennspannung σ nimmt ab, und die Probe bricht im Punkt f.
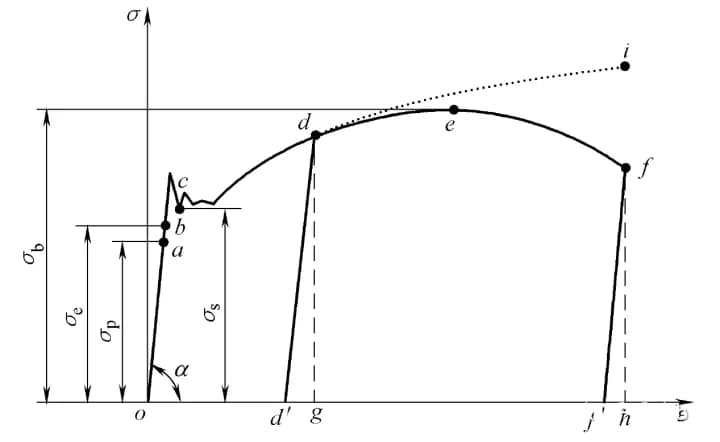
Die Streckgrenze (σs) und die Zugfestigkeit (σb) sind wichtige Indikatoren für die Festigkeit von Werkstoffen mit guter Plastizität (z. B. Stahl mit niedrigem Kohlenstoffgehalt).
Es ist zu beachten, dass die Nennspannung verwendet wird und die mit der Dehnungsverformung einhergehende Verringerung der Querschnittsfläche nicht berücksichtigt wird.
Die Zugfestigkeit (σb) ist nur die nominelle Höchstspannung, die das Material aushalten kann, nicht die tatsächliche Höchstspannung im Inneren des Materials.
Wenn die tatsächliche Fläche der Probe zum Zeitpunkt des Bruchs gemessen wird, ist die tatsächliche maximale Spannung der Spannungswert, der dem Punkt i auf dem Segment der Linie d-i in der Abbildung entspricht.
In der technischen Praxis wird der Einfachheit, Praktikabilität und Sicherheit halber immer noch die Zugfestigkeit (σb) verwendet, um die maximale Spannung darzustellen, die das Material aushalten kann.
Bei der Simulation des nichtlinearen mechanischen Verhaltens von Werkstoffen mit einem Computer muss jedoch die reale Spannungs-Dehnungs-Kurve verwendet werden.
Bei Metallen ohne signifikante Fließerscheinungen kann ihre Zugfestigkeit unter vorgeschriebener nichtproportionaler Dehnung oder Restzugspannung gemessen werden.
Bei Metallen mit signifikantem Fließverhalten können die Streckgrenze, die obere Streckgrenze und die untere Streckgrenze gemessen werden.
Es gibt zwei Methoden zur Messung der oberen und unteren Streckgrenze: die grafische Methode und die Zeigermethode.
Grafische Methode
Während des Versuchs wird mit Hilfe eines automatischen Aufzeichnungsgeräts eine Kraft-Kiefer-Weg-Kurve erstellt.
Das Verhältnis zwischen der Kraftachse und der durch jeden Millimeter repräsentierten Spannung sollte weniger als 10 N/mm betragen.2und die Kurve sollte mindestens bis zum Ende der Fließphase gezogen werden.
Auf der Kurve werden die konstante Kraft Fe während des Nachgebens, die maximale Kraft Feh vor dem ersten Kraftabfall während der Nachgiebigkeitsphase oder die minimale Kraft FeL vor der ersten Momentanwirkung bestimmt.
Die Streckgrenze, die obere Streckgrenze und die untere Streckgrenze können anhand der folgenden Formeln berechnet werden:
Formel zur Berechnung der Streckgrenze: Re = Fe/So; Fe ist die konstante Kraft während des Streckens.
Formel zur Berechnung der oberen Streckgrenze: Reh = Feh/So; Feh ist die maximale Kraft vor dem ersten Kraftabfall in der Fließphase.
Formel zur Berechnung der unteren Streckgrenze: ReL = FeL/So; FeL ist die Mindestkraft vor der ersten Momentanwirkung.
Zeiger-Methode
Wenn der Zeiger des Kraftmessers während des Versuchs bei der konstanten Kraft bzw. der maximalen Kraft vor der ersten Rückkehr oder der minimalen Kraft vor der anfänglichen sofortigen Wirkung aufhört, sich zu drehen, entsprechen sie der Streckgrenze, der oberen Streckgrenze bzw. der unteren Streckgrenze.
Die internen Faktoren, die die Streckgrenze beeinflussen, sind: Bindung, Mikrostruktur, Struktur und atomare Beschaffenheit.
Ein Vergleich der Ausbeute Festigkeit von Metallen mit Keramiken und Polymeren zeigt, dass die Wirkung der Bindung von grundlegender Bedeutung ist.
Was die Auswirkungen der Mikrostruktur betrifft, so gibt es vier Verfestigungsmechanismen, die die Streckgrenze von Metallwerkstoffen beeinflussen, und zwar
(1) Stärkung der festen Lösung;
(2) Kaltverfestigung;
(3) Verstärkung der Ausfällung und Verstärkung der Dispersion;
(4) Verfestigung der Korngrenzen und des Feinkorns. Ausscheidungshärtung und Feinkornhärtung sind die am häufigsten verwendeten Mittel zur Verbesserung der Streckgrenze von Industrielegierungen.
Von diesen Verfestigungsmechanismen erhöhen die ersten drei Mechanismen die Festigkeit des Materials und verringern gleichzeitig die Plastizität.
Nur eine Verfeinerung der Korngröße und des Subkorns kann die Festigkeit und Plastizität des Materials erhöhen.
Die äußeren Faktoren, die die Streckgrenze beeinflussen, sind: Temperatur, Dehnungsgeschwindigkeit und Spannungszustand.
Mit abnehmender Temperatur und zunehmender Dehnungsgeschwindigkeit nimmt die Streckgrenze des Materials zu, insbesondere kubisch-raumzentrierte Metalle reagieren besonders empfindlich auf Temperatur und Dehnungsgeschwindigkeit, was zum Sprödbruch von Stahl bei niedrigen Temperaturen führt.
Der Einfluss des Spannungszustandes ist ebenfalls wichtig. Obwohl die Streckgrenze die inhärente Leistung eines Materials widerspiegelt, ist der Wert der Streckgrenze auch vom Spannungszustand abhängig.
Als Streckgrenze eines Werkstoffs wird im Allgemeinen die Streckgrenze unter einachsiger Spannung bezeichnet.
| Stahlsorte | Mechanische Eigenschaften | Chemische Zusammensetzung | ||||||||
| Streckgrenze | Zugfestigkeit | Dehnung | C | Si | Mn | S | P | |||
| MPa | kg/mm2 | MPa | Kg/mm2 | mm | Kleiner als oder gleich. | Kleiner als oder gleich. | Kleiner als oder gleich. | |||
| Q215A Q215B | 215 | 22 | 335-410 | 3442 | 31 | 0.09-0.15 | 0.03 | 0.25-0.55 | 0.050 0.045 | 0.045 |
| Q235A Q235B Q235C Q235D | 235 | 24 | 375-460 | 38-47 | 26 | 0.14-0.22 0.12-0.20 ≤0.18 ≤0.17 | 0.30 | 0.30-0.65 0.30-0.70 0.35-0.80 0.35-0.80 | 0.5 0.45 0.40 0.035 | 0.045 0.045 0.040 0.035 |
| Mn (Q345B) | 345 | 35 | 510-600. | 51.60 | 22 | 0.12-0.200 | .20-0.55 | 1.2-1.6 | 0.045 | 0.045 |
Die Prüfung der Streckgrenze ist ein wichtiger Indikator für die Festigkeitseigenschaften von Materialien und ein entscheidender Indikator für die Leistungsfähigkeit von Materialien.
Sie wird häufig zur Bewertung der Oberflächenfestigkeit und des plastischen Verhaltens von Materialien verwendet.
Die Methoden der Streckgrenzenprüfung werden im Allgemeinen in zwei Arten unterteilt: mechanische und nicht-mechanische.
Mechanische Streckgrenzenprüfung:
Diese Methode umfasst im Allgemeinen die Drei-Punkt-Biegemethode, die Zugprüfmaschinenmethode und die Druckmethode. Die Probe wird zwischen zwei Stützen platziert und mit einer mechanischen Vorrichtung wird eine konstante Kraft ausgeübt, um die Streckgrenze zu bestimmen.
Nichtmechanische Streckgrenzenprüfung:
Diese Methode umfasst im Allgemeinen Zug-, Druck- und Torsionsverfahren. Die Probe wird auf dem Prüfgerät befestigt und eine konstante Kraft wird mit Hilfe eines Hebels oder einer Computersteuerung aufgebracht, um die Streckgrenze zu bestimmen.
Um die Genauigkeit und Präzision der Streckgrenzenprüfung zu verbessern, ist es im Allgemeinen notwendig, mehrere Prüfungen unter den erforderlichen Bedingungen durchzuführen und den Durchschnittswert zu ermitteln.
Bei allen Versuchen muss die Behandlung der Probe standardisiert und vollständig sein, und die Probe muss unter der aufgebrachten Kraft konstant gehalten werden. Die ermittelte endgültige Streckgrenze ist die maximale Festigkeit, bei der sich das Material unter der aufgebrachten Last biegen kann.
Durch das Studium dieses Artikels haben wir gelernt, was Streckgrenze ist, die Grundlagen von Spannung und Dehnung, Methoden zur Bestimmung der Streckgrenze, Faktoren, die die Streckgrenze beeinflussen, und Anwendungen der Streckgrenze.
Wir hoffen, dass diese Informationen für alle hilfreich sind.
Wenn Sie Fragen haben, können Sie uns diese gerne in den Kommentaren stellen.
Als Gründer von MachineMFG habe ich mehr als ein Jahrzehnt meiner Karriere der metallverarbeitenden Industrie gewidmet. Meine umfangreiche Erfahrung hat es mir ermöglicht, ein Experte auf den Gebieten der Blechverarbeitung, der maschinellen Bearbeitung, des Maschinenbaus und der Werkzeugmaschinen für Metalle zu werden. Ich denke, lese und schreibe ständig über diese Themen und bin stets bestrebt, in meinem Bereich an vorderster Front zu bleiben. Lassen Sie mein Wissen und meine Erfahrung zu einem Gewinn für Ihr Unternehmen werden.
DE 
EN 
ES 
RU 