Понимание прочности и жесткости в механике материалов

Предисловие

Чтобы обеспечить оптимальную производительность и надежность механической системы или конструкции, каждый компонент должен эффективно и качественно выполнять свои функции. Основная цель проектирования безопасности инженерных компонентов - гарантировать, что все элементы обладают достаточной прочностью, жесткостью и устойчивостью, обеспечивая тем самым общую целостность и долговечность системы.

Стабильность - это фундаментальное понятие в машиностроении, означающее способность компонента сохранять или восстанавливать свое первоначальное равновесное состояние под воздействием внешних сил. Этот принцип имеет решающее значение в различных сценариях, таких как:

1. Внезапный боковой прогиб тонкой колонны при осевом сжатии (Эйлерово смятие)
2. Обрушение колонны здания из-за разрушения несущей конструкции (нестабильность конструкции)
3. Смятие тонкостенных конструкций под действием сжимающих или сдвигающих напряжений (локальное или глобальное смятие)

Эти примеры иллюстрируют важность устойчивости для предотвращения катастрофических отказов и обеспечения безопасной работы механических систем и конструкций.

В этом обсуждении я сосредоточусь на разъяснении моего всестороннего понимания двух одинаково важных инженерных принципов: жесткости и прочности. Эти понятия, наряду с устойчивостью, образуют триаду фундаментальных соображений при проектировании безопасности компонентов, каждый из которых играет жизненно важную роль в определении общей производительности, долговечности и безопасности инженерных систем.

Прочность

Что такое сила?

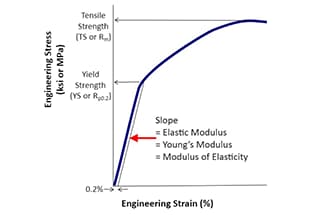
Определение: Прочность - это способность материалов, компонентов или конструкций выдерживать приложенные нагрузки или силы без разрушения, чрезмерной деформации или повреждения. Это фундаментальное свойство в материаловедении и инженерии, определяющее способность материала сопротивляться механическим нагрузкам.

Сила включает в себя различные аспекты, в том числе:

1. Прочность на растяжение: Максимальное напряжение, которое материал может выдержать под действием растягивающих усилий до разрушения.
2. Прочность на сжатие: Максимальное напряжение, которое материал может выдержать под действием сжимающих сил до разрушения.
3. Предел текучести: Напряжение, при котором материал начинает пластически деформироваться.
4. Прочность на сдвиг: Способность противостоять силам, которые вызывают внутреннее скольжение материала вдоль плоскости, параллельной направлению силы.

Например, при изготовлении металлоконструкций понимание прочности материалов имеет решающее значение для проектирования компонентов, способных выдерживать эксплуатационные нагрузки. Стальная балка в здании должна обладать достаточной прочностью, чтобы выдерживать вес конструкции и дополнительные нагрузки, не прогибаясь и не ломаясь.

На прочность влияют различные факторы, в том числе:

• Состав материала и микроструктура
• Методы термообработки и обработки
• Условия окружающей среды (температура, коррозия)
• Скорость и продолжительность загрузки

Единица измерения прочности обычно выражается в мегапаскалях (МПа) или фунтах на квадратный дюйм (psi) в имперских единицах. Например, прочность на растяжение низкоуглеродистой стали составляет примерно 400-550 МПа, в то время как прочность высокопрочных легированных сталей может превышать 1000 МПа.

В производстве и машиностроении расчеты и испытания на прочность имеют большое значение:

• Выбор подходящих материалов для конкретного применения
• Разработка компонентов с оптимальными характеристиками и коэффициентами безопасности
• Прогнозирование срока службы изделий и режимов отказов
• Обеспечение соответствия отраслевым стандартам и нормам

Для оценки и подтверждения прочности материалов и компонентов в сложных инженерных системах часто используются такие передовые методы, как анализ методом конечных элементов (FEA) и разрушающие испытания.

Виды разрушения в зависимости от прочности

Хрупкое разрушение: Внезапный и катастрофический режим разрушения, характеризующийся быстрым распространением трещины при минимальной пластической деформации. Этот тип разрушения происходит без предупреждения и обычно приводит к образованию чистой, плоской поверхности разрушения.

Например:

1. Резкое разрушение чугунного образца вдоль его поперечного сечения при одноосном испытании на растяжение, при котором на поверхности излома образуется кристаллическая масса.
2. Внезапное разрушение чугунного образца с круглым поперечным сечением в косой плоскости при испытании на кручение, демонстрирующее спиралевидную форму разрушения.

Пластическая текучесть: Способ разрушения, при котором материал подвергается значительной пластической деформации, приводящей к необратимому изменению формы и потере структурной целостности. Этот тип разрушения обычно более постепенный и наблюдаемый по сравнению с хрупким разрушением.

Например:

1. При испытании на растяжение образец из низкоуглеродистой стали демонстрирует значительное утолщение и удлинение перед окончательным разрушением с характерной чашечно-конусообразной поверхностью излома.
2. При кручении образец из низкоуглеродистой стали испытывает значительную угловую деформацию и коробление до разрушения, что часто сопровождается видимыми искажениями поверхности.

Важно отметить, что режим разрушения материала зависит от различных факторов, включая свойства материала, условия нагружения, температуру и факторы окружающей среды. Некоторые материалы могут демонстрировать переход от вязкого к хрупкому поведению при определенных условиях, таких как низкие температуры или высокие скорости деформации.

Теория прочности

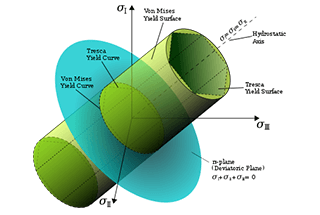
1. Теория максимального растягивающего напряжения:

Когда максимальное растягивающее напряжение σ1 в точке элемента достигает предельного напряжения σb в условиях однонаправленного напряжения, материал подвергается хрупкому разрушению. Таким образом, критерии хрупкого разрушения деталей с критическими точками в условиях сложного напряженного состояния: σ1 = σb.

Следовательно, условия прочности, установленные первым теория прочности являются: σ1 ≤ σb.

2. Теория максимальной деформации при растяжении:

Когда максимальная деформация растяжения ε1 достигает предельного значения εu в условиях однонаправленного напряжения, материал разрушается из-за хрупкого разрушения. Это можно выразить как ε1 = εu.

Исходя из обобщенного закона Гука, мы можем вычислить ε1 как: ε1 = [σ1 - u(σ2 + σ3)] / E, поэтому σ1 - u(σ2 + σ3) = σb.

Условия прочности, установленные второй теорией прочности, таковы: σ1 - u(σ2 + σ3) ≤ σb.

3. Теория максимального напряжения сдвига:

Когда максимальное напряжение сдвига τMax достигает предельного напряжения сдвига τ0 в условиях однонаправленного напряжения, материал разрушается из-за текучести. Это можно выразить как τMax = τ0.

Формула для напряжения сдвига в наклонном сечении при осевом растяжении: τ0 = σs/2 (σs - нормальное напряжение в сечении). Формула для τMax равна (σ1 - σ3)/2. Таким образом, условие повреждения можно переписать как σ1 - σ3 = σs.

Условие прочности, установленное третьей теорией прочности, таково: σ1 - σ3 ≤ σs.

4. Теория удельной энергии изменения формы:

Когда коэффициент изменения формы в какой-либо точке элемента достигает предельного значения в условиях однонаправленного напряжения, материал разрушается из-за текучести.

Условие прочности, установленное четвертой теорией прочности, таково:

√(σ1^2 + σ2^2 + σ3^2 - σ1σ2 - σ2σ3 - σ3σ1) < σs.

2. Жесткость

Что такое жесткость

Определение: Жесткость - это способность материала, компонента или конструкции сопротивляться упругой деформации или смещению при воздействии внешней силы. Она определяет степень, в которой система может сохранять свою форму и размеры в допустимых пределах под действием приложенных нагрузок.

Жесткость - это фундаментальный параметр в машиностроении, который характеризует связь между силой и деформацией в материале или конструкции. Она определяется как отношение приложенной силы к результирующему перемещению, что указывает на количество силы, необходимое для создания единицы деформации. В математическом выражении жесткость (k) выражается как:

k = F / δ

Где:

• F = приложенная сила
• δ = результирующее смещение

Единицей жесткости обычно является сила на единицу длины, например, Н/м (Ньютоны на метр) в системе СИ или фунт-сила на дюйм в имперской системе.

С практической точки зрения жесткость можно осмыслить, используя аналогию с пружиной. Постоянная пружины, которая представляет собой жесткость пружины, определяется как отношение приложенной растягивающей или сжимающей силы к результирующему удлинению или сжатию. Это отношение описывается законом Гука для линейных упругих систем.

Понимание и управление жесткостью имеет решающее значение для различных инженерных приложений, включая:

1. Структурное проектирование: Обеспечение того, чтобы здания и мосты могли выдерживать нагрузки без чрезмерной деформации
2. Механические компоненты: Проектирование деталей, сохраняющих точность при рабочих нагрузках
3. Управление вибрацией: Управление динамической реакцией систем на циклические нагрузки
4. Выбор материала: Выбор подходящих материалов для конкретного применения на основе их жесткостных свойств

Инженерам приходится балансировать между требованиями к жесткости и другими конструктивными соображениями, такими как прочность, вес, стоимость и технологичность, чтобы создавать оптимальные решения для конкретных применений.

Тип жесткости:

Когда приложенная нагрузка постоянна, это называется статической жесткостью.

Когда нагрузка чередуется, это называется динамической жесткостью.

Статическая жесткость включает в себя структурную жесткость и контактную жесткость.

Конструктивная жесткость относится к жесткости самой конструкции и включает в себя жесткость на изгиб и жесткость на кручение.

1. Жесткость на изгиб: рассчитывается по следующей формуле:

K=P/δ

Где

• P - статическая нагрузка (n);
• δ-- Упругая деформация в направлении нагрузки（ μm)。

2. Жесткость на кручение рассчитывается по следующей формуле:

K_m=ML/θ

Где M - приложенный крутящий момент (n - m);

L - расстояние от места приложения крутящего момента до неподвижного конца (м);

θ - Угол скручивания (°)

3. Взаимосвязь между прочностью и жесткостью

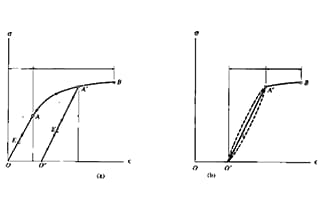
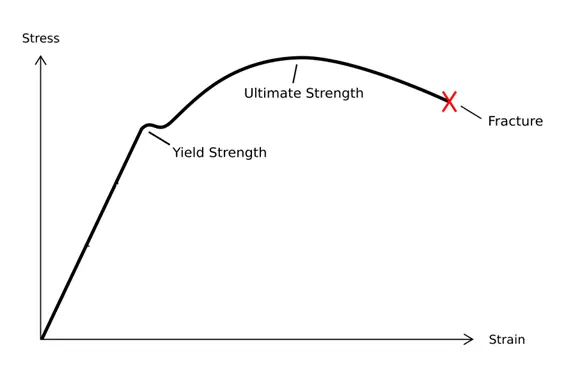
Из приведенного выше объяснения прочности и жесткости видно, что прочность сосредоточена на разрушении под действием внешней силы и подразделяется на пластическую текучесть и хрупкое разрушение, что связано с кривой напряжения-деформации при испытании на растяжение. В отличие от этого, жесткость относится к взаимосвязи между деформацией и силой.

Как показано на рис.

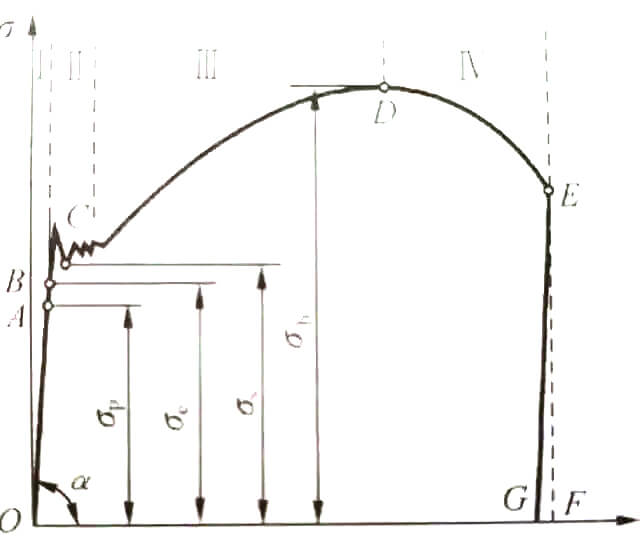
Кривую, изображенную на рисунке, можно разделить на четыре этапа:

1. Стадия упругой деформации;

2. Стадия урожайности;

3. Стадия укрепления;

4. Стадия локального омертвения.

Жесткость определяется как сопротивление упругой деформации, которая возникает на начальном этапе и подчиняется закону Гука в условиях упругости.

Расчет жесткости на изгиб и жесткости на кручение при статические нагрузки схож с законом Гука, что говорит о том, что жесткость измеряется только на стадии упругой деформации.

На следующем этапе, когда во время испытания на растяжение происходит пластическая деформация, остаточная деформация не исчезает. На кривой "напряжение-деформация", хотя напряжение остается почти неизменным, деформация значительно возрастает. В этот момент напряжение достигает предела текучести, и материал переходит в стадию пластического разрушения. По мере того как напряжение продолжает расти, деформация также увеличивается, пока не достигнет предела прочности.

Поэтому измерение прочности происходит после того, как материал подвергся упругой деформации и до того, как он достигнет предела прочности.

Заверните его

В заключение следует отметить, что на стадии разрушения деталей оцениваются как жесткость, так и прочность, причем жесткость измеряется напряжением, а прочность - деформацией.

С точки зрения порядка их следования в процессе деформации, жесткость возникает на более ранней стадии, а прочность - на более поздней.

Таким образом, при оценке условий разрушения деталей, при условии соблюдения требований к жесткости, деталь должна выдерживать достаточные напряжения на этапе упругой деформации, что, в свою очередь, должно соответствовать требованиям к прочности.

Эта взаимосвязь отражается в различных конструкциях, например, в валах механического оборудования. Как правило, размер вала определяется исходя из условий прочности, а затем проверяется его жесткость исходя из условий жесткости.

Поэтому требования к жесткости валов точных машин очень высоки, и при проектировании размеров их поперечного сечения часто руководствуются условиями жесткости.