مخطط بدل الانحناء من 0 درجة إلى 180 درجة لثني الصفائح المعدنية
هل تساءلت يومًا كيف يتم تصميم أجزاء الصفائح المعدنية وتصنيعها بدقة؟ في منشور المدونة هذا، سوف نغوص في عالم بدل الانحناء الرائع - وهو أمر بالغ الأهمية...
هل تساءلت يومًا عن كيفية حساب بدل الانحناء بدقة لمشاريع تصنيع المعادن الخاصة بك؟ في منشور المدونة هذا، سنستكشف العالم الرائع لصيغ وحسابات بدل الانحناء. بصفتي مهندسًا ميكانيكيًا متمرسًا، سأرشدك إلى المفاهيم الأساسية وأقدم لك رؤى عملية لمساعدتك على إتقان هذا الجانب المهم من تصميم الصفائح المعدنية. استعد للغوص واكتشاف أسرار إنشاء انحناءات دقيقة وفعالة في مشاريعك!
بدل الانحناء هو مفهوم مهم في مجال تصنيع الصفائح المعدنية، خاصةً عند العمل في عمليات الثني. وهو يشير إلى طول المادة الإضافي المطلوب لاستيعاب الانحناء في الصفيحة المعدنية. يعد فهم بدل الانحناء وحسابه بدقة أمرًا ضروريًا لضمان مطابقة الأبعاد النهائية للجزء المثني لمواصفات التصميم.
تُعد الحسابات الدقيقة لبدلات الانحناء أمرًا حيويًا في عملية التصنيع. عندما يتم ثني صفيحة معدنية مسطحة، تتمدد المادة الموجودة على السطح الخارجي للثني، بينما تنضغط المادة الموجودة في الداخل. وبدون حساب هذا التشوه، لن يتطابق المنتج النهائي مع التصميم المقصود، مما يؤدي إلى عدم الدقة والفشل المحتمل. تساعد بدلات الانحناء المصنّعين على ضبط أبعاد النمط المسطح، مما يضمن أن الجزء المثني يلبي المتطلبات الدقيقة.
تؤثر العديد من المعلمات الحرجة على حسابات بدل الانحناء:
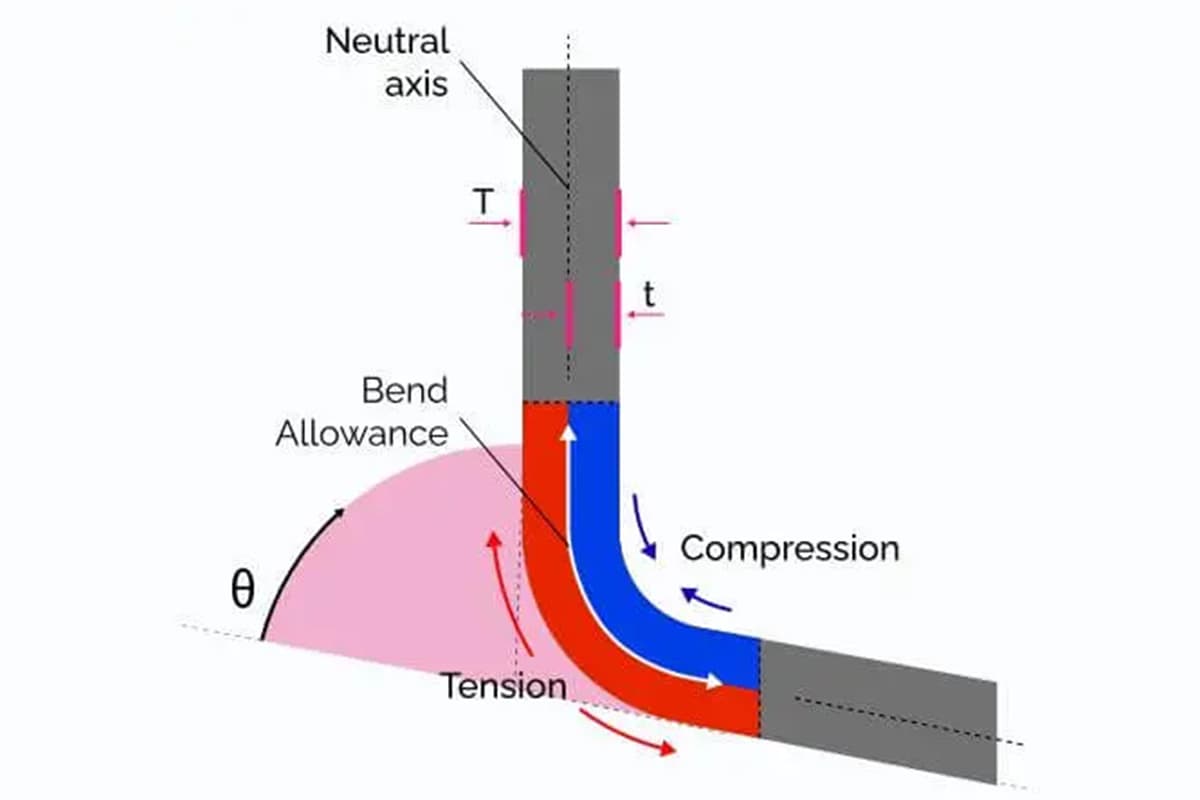
مفهوم بدل الانحناء هي كما يلي: عندما يتم ثني صفيحة معدنية، يكون لها ثلاثة أبعاد - بعدان خارجيان (L1 وL2) وبُعد سمك واحد (T).
من المهم ملاحظة أن مجموع (L1) و(L2) أكبر من الطول غير المطوي (L)، والفرق بين الاثنين يعرف ببدل الانحناء (K).
ومن ثم، يمكن حساب الطول غير المطوي للانحناء على النحو التالي L = L1 + L2 - K.
قراءة ذات صلة:
كيف كانت صيغة بدل الانحناء التي تم إنشاؤها؟ وكيف تحسب بدل الانحناء?
يعتمد بدل الانحناء على نصف القطر الداخلي المُشكَّل. تحدد الفتحة السفلية للقالب V السفلي نصف القطر الداخلي (I.R.) للجزء المُشكَّل. يساوي نصف القطر الداخلي للفولاذ الطري 5/32 × فتحة القالب السفلي للقالب على شكل حرف V (W) عندما يكون نصف قطر المثقاب أقل من 5/32 × W.
إذا كانت I.R.< سماكة المادة (t)
إذا كان I.R.> 2 × سُمك المادة (t)
حيث A= (180 - زاوية الانحناء المتضمنة)
إذا كان نصف القطر الداخلي يساوي t أو 2t، أو بين t و2t، يتم حساب بدل الانحناء عن طريق استيفاء قيم بدل الانحناء من الصيغتين المذكورتين أعلاه.
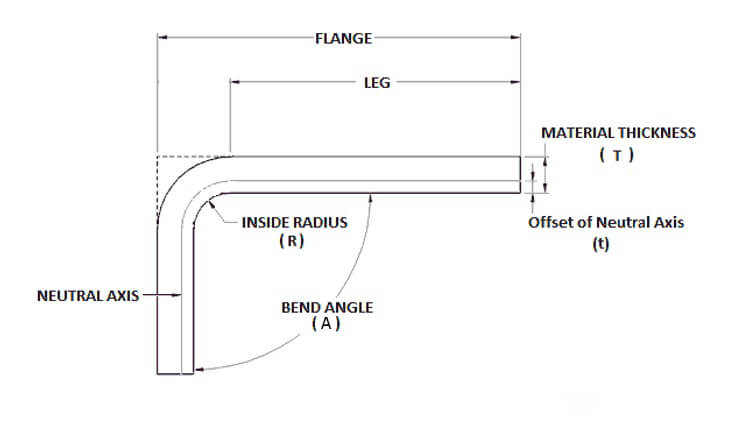
بالإضافة إلى ذلك، لحساب بدل الانحناء هذا، يمكنك أيضاً استخدام الصيغة التالية:
تراعي هذه الصيغة الأشكال الهندسية والخصائص المتنوعة للأجزاء المراد تشكيلها.
سُمك المادة (T)، وزاوية الانحناء (A)، والجزء الداخلي نصف قطر الانحناء (R)، وعامل K للمادة المراد ثنيها هما العاملان الأكثر أهمية في هذه العملية الحسابية.
كما يتضح من الصيغة أعلاه، فإن حساب بدل الانحناء عملية بسيطة.
يمكنك تحديد بدل الانحناء عن طريق التعويض بالقيم المذكورة أعلاه في الصيغة.
عندما تكون زاوية الانحناء 90 درجة، يمكن تبسيط معادلة بدل الانحناء على النحو التالي:
ملاحظة: يقع عامل K لمعظم المواد والسماكات القياسية عادةً بين 0 و0.5.
يمكنك حساب قيمة عامل K بدقة باستخدام ما يلي حاسبة العامل K:
تُعد معادلة بدل الانحناء (BA) ضرورية لحساب طول المادة المطلوبة لتشكيل الانحناء. هذه المعادلة العامة قابلة للتطبيق على نطاق واسع في مختلف المواد وطرق الانحناء:
أين:
يعتبر العامل K عامل حاسم لأنه يشير إلى موضع المحور المحايد الذي لا يتغير طوله أثناء الانحناء. وعادةً ما يتراوح عامل K بين 0.3 و0.5 ويختلف بناءً على نوع المادة والسُمك ونصف القطر وطريقة الثني.
المواد المختلفة لها خصائص فريدة تستلزم إجراء تعديلات على حسابات بدل الانحناء. تضمن هذه التعديلات الدقة، خاصةً عند الانحناءات بزاوية 90 درجة:
بالنسبة للمواد الأكثر ليونة مثل النحاس الأصفر أو النحاس اللين، يتم حساب بدل الانحناء على النحو التالي:
ba = (0.55 × t) + (1.57 × r)
ويراعي هذا التعديل ليونة المادة وانخفاض مقاومتها للتشوه.
بالنسبة للنحاس شبه الصلب أو النحاس الأصفر والنحاس الأصفر، والصلب اللين، والألومنيوم، تكون بدل الانحناء:
BA = (0.64 × T) + (1.57 × R)
تتميز هذه المواد بصلابة معتدلة، مما يتطلب بدلًا أعلى قليلاً من المواد الأكثر ليونة.
بالنسبة للمواد الأكثر صلابة مثل البرونز والنحاس الصلب والفولاذ المدلفن على البارد والفولاذ الزنبركي، تكون المعادلة هي
BA = (0.71 × T) + (1.57 × R)
تكون هذه المواد أكثر مقاومة للانحناء، مما يستلزم بدل أعلى.
لتحديد إجمالي الطول المسطح لجزء الصفيحة المعدنية، يتم إضافة بدل الانحناء إلى أطوال الأجزاء المسطحة:
طول الساق المسطح = طول الساق 1 + BA + طول الساق 2
يضمن هذا النهج دقة أبعاد الجزء النهائي بعد الثني.
ضع في اعتبارك ثني بزاوية 90 درجة في صفيحة ألومنيوم بسُمك 2 مم ونصف قطر ثني داخلي 5 مم. باستخدام المعادلة الخاصة بالمادة للنحاس شبه الصلب والنحاس الأصفر والصلب اللين والألومنيوم:
ب أ = (0.64 × 2) + (1.57 × 5)
BA = 1.28 + 7.85=9.13
إذا كان الجزء يحتوي على جزأين مسطحين طول كل منهما 50 مم، فإن إجمالي طول المسطح سيكون:
الطول المسطح = 50 + 9.13 + 50 = 109.13 مم
وبالإضافة إلى بدل الانحناء، فإن خصم الانحناء (BD) والانتكاسة الخارجية (OSSB) مهمان لإجراء قياسات دقيقة:
خصم الانحناء (BD) = OSSB - BA
أين:
تعد هذه التركيبات والاعتبارات ضرورية لحساب بدلات الانحناء بدقة، مما يضمن تصنيع أجزاء الصفائح المعدنية بالأبعاد والملاءمة الصحيحة.
يُعد بدل الانحناء عاملًا حاسمًا في عملية ثني الصفائح المعدنية، خاصةً بالنسبة لمواد مثل الألومنيوم. فهو يمثل تمدد المادة الذي يحدث أثناء الثني، مما يضمن دقة الأبعاد النهائية. سنناقش هنا الصيغة المحددة المستخدمة لألواح الألومنيوم وتطبيقها.
يمكن حساب بدل الانحناء للوح الألومنيوم باستخدام المعادلة التالية:
𝐿=𝐿1+𝐿2-1.6 𝑇-1.6
أين:
يتم اشتقاق القيمة 1.6𝑇 تجريبياً، بمعنى أنه تم تحديدها من خلال التجربة العملية وخبرة الإنتاج. ويراعي هذا العامل سلوك المادة أثناء الثني، مما يضمن دقة الأبعاد النهائية.
من المهم ملاحظة أن هذه الصيغة تنطبق على وجه التحديد في ظل ظروف معينة:
لتحديد الحجم الموسع للوح الألومنيوم، اتبع الخطوات التالية:
ستعطيك هذه العملية الحسابية طول النمط المسطح المطلوب قبل الثني، مما يضمن أن الجزء المثني النهائي له الأبعاد الصحيحة.
تعمل حاسبة بدل الانحناء الواردة أدناه على تبسيط عملية حساب قيمة بدل الانحناء، وهو أمر بالغ الأهمية لتصنيع الصفائح المعدنية بدقة. بدل الانحناء هو طول المحور المحايد بين خطوط الانحناء، وهو ما يساعد في تحديد حجم الفراغ الصحيح للجزء المنحني.
تُعد زاوية الانحناء، التي يُشار إليها بـ θ، معلمة حاسمة في معادلة بدل الانحناء. وهي تمثل الزاوية التي يتم من خلالها ثني الصفيحة المعدنية. تُقاس زاوية الانحناء عادةً بالدرجات ولكن يمكن تحويلها إلى راديان باستخدام المعادلة:
نصف القطر الداخلي، الممثل بالرمز r، هو نصف قطر المنحنى الداخلي للانحناء. يؤثر نصف القطر هذا بشكل مباشر على مقدار التمدد والانضغاط الذي يحدث داخل المادة أثناء الانحناء. يؤدي نصف القطر الداخلي الأصغر إلى تشوه أكبر، وهو ما يجب أخذه في الحسبان عند حساب بدل الانحناء.
سمك المادة، المشار إليه بالرمز T، هو سمك الصفيحة المعدنية التي يتم ثنيها. تواجه المواد الأكثر سمكًا تمددًا وانضغاطًا أكثر وضوحًا، مما يؤثر على بدل الانحناء الكلي. القياس الدقيق لسُمك المادة ضروري لإجراء حسابات دقيقة لبدلات الانحناء المسموح بها.
عامل K هو قيمة بلا أبعاد تمثل موضع المحور المحايد بالنسبة إلى سُمك المادة. المحور المحايد هو الخط النظري داخل المادة الذي يظل طوله دون تغيير أثناء الانحناء. ويختلف عامل K بناءً على خصائص المادة وطرق الانحناء، ويتراوح عادةً من 0.3 إلى 0.5 لمعظم المواد. معادلة موضع المحور المحايد هي:
وضع المحور المحايد = K × T
المحور المحايد هو الخط الوهمي داخل المادة الذي يظل طوله دون تغيير أثناء الانحناء. إن فهم موضعه أمر بالغ الأهمية لحساب بدل الانحناء الصحيح.
بدل الانحناء، الممثل ب BA، هو طول المحور المحايد المطلوب لتشكيل الانحناء. ويُحسب باستخدام المعادلة:
تستخدم هذه المعادلة زاوية الانحناء، ونصف القطر الداخلي، وسُمك المادة، وعامل K لضمان دقة حسابات بدل الانحناء.
يُعد مخطط بدلات الانحناء مورداً أساسياً للمحترفين العاملين في تصنيع الصفائح المعدنية. فهو يوفر قائمة شاملة للمعلمات الرئيسية مثل سُمك المادة، ونصف قطر الانحناء، وزاوية الانحناء، وبدل الانحناء، وقيم خصم الانحناء للمواد الشائعة. هذه المعلومات ضرورية لحساب طول تطوير جزء الصفيحة المعدنية بعد الثني بدقة.
المزيد من القراءة:
| التلفاز | الزاوية | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | أقصر حجم |
| V4 | 90 | 0.9 | 1.4 | 2.8 | ||||||||||
| V4 | 120 | 0.7 | ||||||||||||
| V4 | 150 | 0.2 | ||||||||||||
| V6 | 90 | 1.5 | 1.7 | 2.15 | 4.5 | |||||||||
| V6 | 120 | 0.7 | 0.86 | 1 | ||||||||||
| V6 | 150 | 0.2 | 0.3 | 0.4 | ||||||||||
| V7 | 90 | 1.6 | 1.8 | 2.1 | 2.4 | 5 | ||||||||
| V7 | 120 | 0.8 | 0.9 | 1 | ||||||||||
| V7 | 150 | 0.3 | 0.3 | 0.3 | ||||||||||
| V8 | 90 | 1.6 | 1.9 | 2.2 | 2.5 | 5.5 | ||||||||
| V8 | 30 | 0.3 | 0.34 | 0.4 | 0.5 | |||||||||
| V8 | 45 | 0.6 | 0.7 | 0.8 | 1 | |||||||||
| V8 | 60 | 1 | 1.1 | 1.3 | 1.5 | |||||||||
| V8 | 120 | 0.8 | 0.9 | 1.1 | 1.3 | |||||||||
| V8 | 150 | 0.3 | 0.3 | 0.2 | 0.5 | |||||||||
| V10 | 90 | 2.7 | 3.2 | 7 | ||||||||||
| V10 | 120 | 1.3 | 1.6 | |||||||||||
| V10 | 150 | 0.5 | 0.5 | |||||||||||
| V12 | 90 | 2.8 | 3.65 | 4.5 | 8.5 | |||||||||
| V12 | 30 | 0.5 | 0.6 | 0.7 | ||||||||||
| V12 | 45 | 1 | 1.3 | 1.5 | ||||||||||
| V12 | 60 | 1.7 | 2 | 2.4 | ||||||||||
| V12 | 120 | 1.4 | 1.7 | 2 | ||||||||||
| V12 | 150 | 0.5 | 0.6 | 0.7 | ||||||||||
| V14 | 90 | 4.3 | 10 | |||||||||||
| V14 | 120 | 2.1 | ||||||||||||
| V14 | 150 | 0.7 | ||||||||||||
| V16 | 90 | 4.5 | 5 | 11 | ||||||||||
| V16 | 120 | 2.2 | ||||||||||||
| V16 | 150 | 0.8 | ||||||||||||
| V18 | 90 | 4.6 | 13 | |||||||||||
| V18 | 120 | 2.3 | ||||||||||||
| V18 | 150 | 0.8 | ||||||||||||
| V20 | 90 | 4.8 | 5.1 | 6.6 | 14 | |||||||||
| V20 | 120 | 2.3 | 3.3 | |||||||||||
| V20 | 150 | 0.8 | 1.1 | |||||||||||
| V25 | 90 | 5.7 | 6.4 | 7 | 17.5 | |||||||||
| V25 | 120 | 2.8 | 3.1 | 3.4 | ||||||||||
| V25 | 150 | 1 | 1 | 1.2 | ||||||||||
| V32 | 90 | 7.5 | 8.2 | 22 | ||||||||||
| V32 | 120 | 4 | ||||||||||||
| V32 | 150 | 1.4 | ||||||||||||
| V40 | 90 | 8.7 | 9.4 | 28 | ||||||||||
| V40 | 120 | 4.3 | 4.6 | |||||||||||
| V40 | 150 | 1.5 | 1.6 |
| التلفاز | الزاوية | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | أقصر حجم |
| V4 | 1.4 | 2.8 | ||||||||||||
| V6 | 1.6 | 4.5 | ||||||||||||
| V7 | 1.6 | 1.8 | 5 | |||||||||||
| V8 | 1.8 | 2.4 | 3.1 | 5.5 | ||||||||||
| V10 | 2.4 | 3.2 | 7 | |||||||||||
| V12 | 2.4 | 3.2 | 8.5 | |||||||||||
| V14 | 3.2 | 10 | ||||||||||||
| V16 | 3.2 | 4 | 4.8 | 11 | ||||||||||
| V18 | 4.8 | 13 | ||||||||||||
| V20 | 4.8 | 14 | ||||||||||||
| V25 | 4.8 | 5.4 | 6 | 17.5 | ||||||||||
| V32 | 6.3 | 6.9 | 22 |
| الزاوية | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | أقصر حجم |
| 90 | 3.6 | 5.2 | 6.8 | 8.4 | 28 | ||||||||
| 120 | |||||||||||||
| 150 |
| المواد | SPCC | SUS | آل （LY12) | SECC | ||||
|---|---|---|---|---|---|---|---|---|
| T | 𞸍 | Δك | 𞸍 | Δك | 𞸍 | Δك | 𞸍 | Δك |
| T=0.6 | 1.25 | 1.26 | ||||||
| T=0.8 | 0.18 | 1.42 | 0.15 | 1.45 | 0.09 | 1.51 | ||
| T=1.0 | 0.25 | 1.75 | 0.20 | 1.80 | 0.30 | 1.70 | 0.38 | 1.62 |
| T=1.2 | 0.45 | 1.95 | 0.25 | 2.15 | 0.50 | 1.90 | 0.43 | 1.97 |
| T=1.4 | 0.64 | 2.16 | ||||||
| T=1.5 | 0.64 | 2.36 | 0.50 | 2.50 | 0.70 | 2.30 | ||
| T=1.6 | 0.69 | 2.51 | ||||||
| T=1.8 | 0.65 | 3.00 | ||||||
| T=1.9 | 0.60 | 3.20 | ||||||
| T=2.0 | 0.65 | 3.35 | 0.50 | 3.50 | 0.97 | 3.03 | 0.81 | 3.19 |
| T=2.5 | 0.80 | 4.20 | 0.85 | 4.15 | 1.38 | 3.62 | ||
| T=3.0 | 1.00 | 5.00 | 5.20 | 1.40 | 4.60 | |||
| T=3.2 | 1.29 | 5.11 | ||||||
| T=4.0 | 1.20 | 6.80 | 1.00 | 7.00 | ||||
| T=5.0 | 2.20 | 7.80 | 2.20 | 7.80 | ||||
| T=6.0 | 2.20 | 9.80 | ||||||
ملاحظة:
يُعد مخطط بدل الانحناء الذي يتم صيانته جيدًا أداة حيوية في صناعة تصنيع الصفائح المعدنية. فهو يضمن الدقة والكفاءة في عملية الانحناء، مما يؤدي في النهاية إلى منتجات نهائية عالية الجودة وأكثر دقة. من خلال فهم واستخدام القيم الواردة في المخطط، يمكن للمهندسين والمصنّعين تحقيق أفضل النتائج في مشاريعهم.
في تصنيع الصفائح المعدنية، يعد تحقيق الدقة والدقة أمرًا بالغ الأهمية لإنشاء أجزاء عالية الجودة. أحد العوامل الرئيسية التي تلعب دورًا هامًا في هذه العملية هو العامل K-Factor. يعد فهم عامل K-Factor وتطبيقه في حسابات بدلات الانحناء أمرًا ضروريًا للمصنعين لإنتاج أجزاء تلبي المواصفات الدقيقة وتؤدي بشكل موثوق في مختلف الصناعات.
عامل K هو قيمة بلا أبعاد تمثل نسبة المسافة من المحور المحايد إلى سُمك المادة. وهي ضرورية لإجراء حسابات دقيقة لبدلات الانحناء، والتي تحدد كمية المادة اللازمة لتحقيق الانحناء المطلوب. المحور المحايد هو خط وهمي داخل المادة لا يتغير طوله أثناء الانحناء. من خلال فهم عامل K-Factor، يمكن للمصنّعين التنبؤ بكيفية تصرف المادة عند الثني، مما يضمن عمليات تصنيع دقيقة وفعالة.
يتم حساب عامل K-Factor باستخدام المعادلة:
أين:
يساعد استخدام عامل K-Factor في معادلة بدل الانحناء في التنبؤ باستطالة المادة وانضغاطها أثناء الانحناء. معادلة بدل الانحناء هي:
لتوضيح ذلك، دعونا نستعرض مثالاً بسيطًا. لنفترض أن لدينا جزءًا من صفيحة معدنية بسُمك (T) 2 مم، مثني بزاوية 90 درجة (θ)، ونصف قطرها الداخلي (r) 5 مم، وعامل K (K) 0.4.
1. حوِّل زاوية الانحناء إلى راديان:
2. تطبيق القيم على معادلة بدل الانحناء:
توضح هذه العملية الحسابية أن هناك حاجة إلى ما يقرب من 9.11 مم من المادة على طول المحور المحايد لتحقيق الانحناء المطلوب، مما يوضح أهمية عامل K الدقيق.
يؤثر عامل K-Factor بشكل مباشر على دقة حسابات بدل الانحناء. يضمن العامل K-Factor الدقيق تطابق الأبعاد النهائية للجزء المثني مع مواصفات التصميم، مما يقلل من هدر المواد والحاجة إلى إعادة العمل. هذه الدقة أمر حيوي للصناعات التي تكون فيها الأبعاد الدقيقة ضرورية لتجميع المكونات ووظائفها.
تتميز المواد المختلفة بخصائص ميكانيكية فريدة من نوعها، مما يؤدي إلى اختلاف قيم عامل K. عادةً ما يكون للمواد الأكثر ليونة مثل الألومنيوم عامل K-عامل أقل، بينما المواد الأكثر صلابة مثل الفولاذ المقاوم للصدأ لها عامل K-عامل أعلى. يسمح فهم هذه الاختلافات للمصنعين باختيار قيم عامل K المناسبة للمواد المختلفة، مما يضمن إجراء حسابات دقيقة وعمليات تصنيع فعالة.
فيما يلي إجابات على بعض الأسئلة المتداولة:
تُستخدم معادلة بدل الانحناء لحساب طول المحور المحايد للانحناء في الصفيحة المعدنية، وهو أمر بالغ الأهمية لتحديد طول النمط المسطح الصحيح قبل ثني المعدن. يضمن هذا الحساب تطابق الأبعاد النهائية للجزء المثني مع مواصفات التصميم.
تأخذ المعادلة في الاعتبار عدة معايير رئيسية:
الصيغة العامة لبدل الانحناء (BA) هي:
باستخدام هذه الصيغة، يمكنك حساب الطول الدقيق للمادة المطلوبة لتشكيل الانحناء، مما يضمن عدم تمدد المادة بشكل مفرط أو انضغاطها أكثر من اللازم. ثم يتم إضافة بدل الانحناء المحسوب هذا إلى أطوال أرجل الجزء لتطوير نمط مسطح دقيق، وهو أمر ضروري لإنتاج أجزاء ذات أبعاد دقيقة.
ترتبط معادلة بدل الانحناء أيضًا بخصم الانحناء، وهو الطول الذي يجب طرحه من الطول الإجمالي للوح المعدني لتحقيق النمط المسطح الصحيح. يتم احتساب خصم الانحناء باستخدام بدل الانحناء والارتداد الخارجي، مما يضمن دقة أبعاد الجزء النهائي بعد الثني.
على سبيل المثال، إذا كنت تقوم بثني صفيحة من الفولاذ المقاوم للصدأ بسُمك 2 مم بزاوية 90 درجة مع نصف قطر انحناء داخلي 3 مم وعامل K 0.44، يمكن حساب بدل الانحناء على النحو التالي:
يتم بعد ذلك استخدام بدل الانحناء هذا لضمان تطوير النمط المسطح بشكل صحيح، مما ينتج عنه جزء يفي بمواصفات التصميم. باختصار، تُعد معادلة بدل الانحناء ضرورية لتصنيع الصفائح المعدنية بدقة، مما يضمن إنتاج الأجزاء النهائية بالأبعاد الصحيحة.
لحساب بدل الانحناء في الصفائح المعدنية، تحتاج إلى تحديد عدة معلمات رئيسية: سُمك المادة (T)، وزاوية الانحناء (θ)، ونصف القطر الداخلي (r)، والعامل K (K). يتم حساب بدل الانحناء (BA) باستخدام المعادلة:
إليك العملية خطوة بخطوة:
باستخدام هذه الصيغة، لنفس المعلمات
باتباع هذه الخطوات واستخدام الصيغة المناسبة، يمكنك حساب بدل الانحناء لأجزاء الصفائح المعدنية بدقة، مما يضمن لك تصنيعًا دقيقًا.
يعتبر العامل K مهمًا في معادلة بدل الانحناء لعدة أسباب، يبرز كل منها أهميته في تصنيع الصفائح المعدنية الدقيقة. أولاً، يمثل نسبة المحور المحايد إلى سُمك المادة. أثناء الانحناء، ينزاح المحور المحايد من موقعه الأصلي عند 50% من سُمك المادة نحو السطح الداخلي للثني. هذا الانزياح أمر بالغ الأهمية لأنه يحدد مقدار الاستطالة التي تحدث في المادة. يساعد عامل K في حساب هذا الموقع الجديد، وهو أمر ضروري لحسابات الانحناء الدقيقة.
ثانيًا، يعتبر العامل K أساسيًا في حساب بدل الانحناء، وهو طول الألياف المحايدة من بداية القوس الناتج عن الانحناء إلى نهايته. هذا الحساب ضروري لتحديد الحجم المسطح للصفائح المعدنية المطلوبة لتحقيق شكل الانحناء المطلوب. ويتأثر بدل الانحناء مباشرةً بعامل K، حيث إنه يأخذ في الحسبان استطالة المادة أثناء عملية الانحناء.
بالإضافة إلى ذلك، يسمح استخدام عامل K بحسابات دقيقة لخصومات الانحناء، والتراجع الخارجي، والتخطيط المسطح الكلي للجزء. هذه الدقة أمر حيوي لأنها تضمن تطابق الأبعاد النهائية للجزء المثني مع مواصفات التصميم، وتجنب الأخطاء التي قد تنشأ من استخدام قيم عامل K عامة أو غير دقيقة.
يختلف عامل K بناءً على عدة بارامترات، بما في ذلك نوع المادة والسُمك وطريقة التشكيل والأدوات وزاوية الانحناء. هذا التباين يعني أن عامل K يجب أن يكون مصممًا وفقًا للظروف المحددة لعملية الانحناء. من خلال مراعاة هذه العوامل، يساعد عامل K في تخصيص معادلة تعويض الانحناء لتحقيق نتائج أكثر دقة.
وأخيرًا، تعتبر القيمة الصحيحة للعامل K ضرورية لتجنب الأخطاء في الأبعاد النهائية للصفيحة المطوية. يمكن أن تؤدي القيم غير الصحيحة للعامل K إلى عدم الدقة في بدلات الانحناء، مما يؤدي إلى أجزاء لا تفي بالمواصفات المطلوبة. لذلك، يعد تحديد عامل K واستخدامه بدقة أمرًا بالغ الأهمية لإنتاج مكونات عالية الجودة.
باختصار، يعتبر عامل K مهمًا لأنه يسمح بحساب دقيق لبدلات الانحناء، ويأخذ في الاعتبار إزاحة المحور المحايد، ويأخذ في الاعتبار معلمات المواد والمعالجة المحددة، وكلها ضرورية لتحقيق نتائج دقيقة وموثوقة في ثني الصفائح المعدنية.
تتضمن معادلة بدل الانحناء في ثني الصفائح المعدنية عادةً العديد من المتغيرات الرئيسية:
يمكن حساب بدل الانحناء (BA) باستخدام المعادلة:
أو
حيث (0.017453) هو (π/180) و(0.0078) هو (π/180) × K) - العامل (π/180) - العامل.
تُعد هذه المتغيرات ضرورية في تحديد بدل الانحناء بدقة، وهو أمر بالغ الأهمية لتصنيع الصفائح المعدنية الدقيقة.
نعم، يمكن أن تختلف معادلة بدل الانحناء اختلافًا كبيرًا بناءً على نوع المادة، بالإضافة إلى عوامل أخرى مثل سُمك المادة وزاوية الانحناء وعملية الانحناء المحددة.
يمثل عامل K، وهو عنصر حاسم في معادلة بدل الانحناء، إزاحة المحور المحايد النظري أثناء الانحناء ويختلف باختلاف المادة. على سبيل المثال، عادةً ما يستخدم الفولاذ الطري المدلفن على البارد عامل K حوالي 0.446، في حين أن المواد الأخرى مثل الفولاذ المقاوم للصدأ والألومنيوم لها عوامل K مختلفة بسبب خصائصها وسلوكيات الانحناء الفريدة.
تتضمن معادلة بدل الانحناء أيضًا سُمك المادة وزاوية الانحناء، والتي يمكن أن تختلف بين المواد. والصيغة العامة لصيغة بدل الانحناء هي:
حيث:
تتميز المواد المختلفة بخصائص مختلفة مثل المرونة وقوة الشد واتجاه الحبيبات التي تؤثر على سلوك الانحناء. على سبيل المثال، ينثني الألومنيوم بسهولة أكبر من الفولاذ، مما يتطلب تعديلات في حساب بدل الانحناء. بالإضافة إلى ذلك، يمكن أن يتطلب ثني المعدن على طول اتجاهه الحبيبي قوة أكبر وبدل ثني مختلف مقارنةً بالثني عبر الحبيبات.
يجب أيضًا مراعاة ميل المادة إلى الارتداد بعد الانحناء، والمعروف باسم الارتداد النابض. ويتضمن ذلك الإفراط في ثني المادة قليلاً لمراعاة الاسترداد المرن، الذي يتأثر بنوع المادة وخصائصها.
باختصار، يجب أن تكون معادلة بدل الانحناء مصممة خصيصًا للمادة المحددة المستخدمة، مع الأخذ في الاعتبار خصائصها الفريدة وسمكها وعملية الانحناء المعنية.
بصفتي مؤسس شركة MachineMFG، فقد كرّستُ أكثر من عقد من حياتي المهنية في مجال تصنيع المعادن. وقد أتاحت لي خبرتي الواسعة أن أصبح خبيرًا في مجالات تصنيع الصفائح المعدنية، والتصنيع الآلي، والهندسة الميكانيكية، وأدوات الماكينات للمعادن. أفكر وأقرأ وأكتب باستمرار في هذه المواضيع، وأسعى باستمرار للبقاء في طليعة مجال عملي. فلتكن معرفتي وخبرتي مصدر قوة لعملك.
AR 
EN 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO