حاسبة عامل Y
كيف يمكنك ثني جزء الصفيحة المعدنية بدقة دون تجربة وخطأ؟ إن العامل Y هو المفتاح. تشرح هذه المقالة العامل Y، وهو ثابت حاسم يُستخدم لحساب معامل Y...
هل تواجه صعوبة في تصميم أجزاء الصفائح المعدنية الدقيقة؟ اكتشف أسرار العامل K، وهو مفهوم حاسم في تصنيع الصفائح المعدنية. في هذه المقالة، يقوم مهندسنا الميكانيكي الخبير بإزالة الغموض عن العامل K، ويشرح علاقته بالطبقة المحايدة ويقدم طرقًا عملية للحساب. اكتشف كيف يمكن أن يؤدي إتقان العامل K إلى إحداث ثورة في تصميمات الصفائح المعدنية وضمان نجاح التصنيع.
تقدم هذه المقالة استكشافًا متعمقًا لعامل K، وهو مفهوم مهم في تصميم وتصنيع الصفائح المعدنية. ويغطي تعريف عامل K، وعلاقته بالطبقة المحايدة، وطرق حساب عامل K ومعايرته.
تناقش المقالة أيضًا العوامل التي تؤثر على عامل K، مثل خواص المواد ومعلمات الانحناء، وتوفر إرشادات عملية لتحديد القيمة المثلى لعامل K لمختلف التطبيقات.
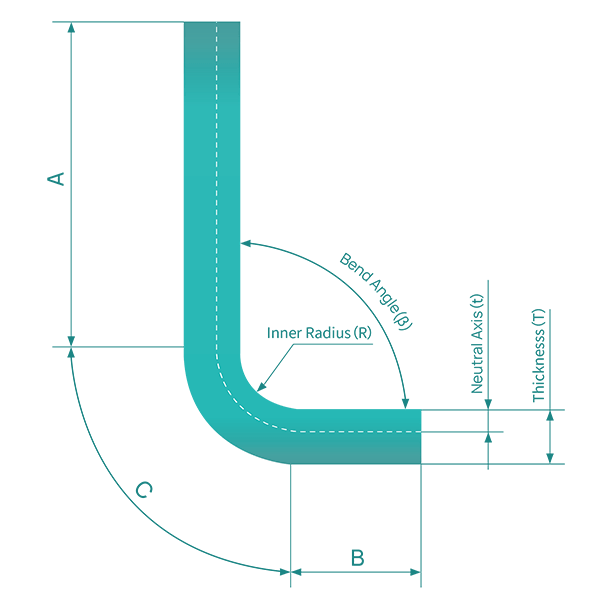
يعتبر العامل K عاملاً حاسمًا في تصميم الصفائح المعدنية وتصنيعها، خاصةً عند العمل باستخدام برامج التصميم بمساعدة الحاسوب مثل SolidWorks. وهو يمثل موقع المحور المحايد داخل الانحناء ويلعب دورًا حيويًا في تحديد الطول الدقيق لأجزاء الصفائح المعدنية بعد الثني. من الناحية الرياضية، يُعرَّف العامل K بأنه نسبة المسافة بين الطبقة المحايدة والسطح الداخلي للثني (t) إلى السُمك الكلي للصفائح المعدنية (T):
ك = ر / ت
تقع هذه القيمة الخالية من الأبعاد دائمًا بين 0 و1، وتتراوح عادةً من 0.3 إلى 0.5 لمعظم المواد الشائعة وعمليات الثني. عامل K ضروري لعدة أسباب:
تشمل العوامل المؤثرة على عامل K خواص المواد (مثل قوة الخضوع والليونة)، وسُمك الصفيحة، ونصف قطر الانحناء، وطريقة الثني (الثني الهوائي، الثني السفلي، الثني بالليونة). غالبًا ما يستخدم التصنيع الحديث للصفائح المعدنية الحديثة جداول عامل K المشتقة تجريبيًا أو تحليل العناصر المحدودة المتقدم (FEA) لتحديد القيم المثلى لتطبيقات محددة.
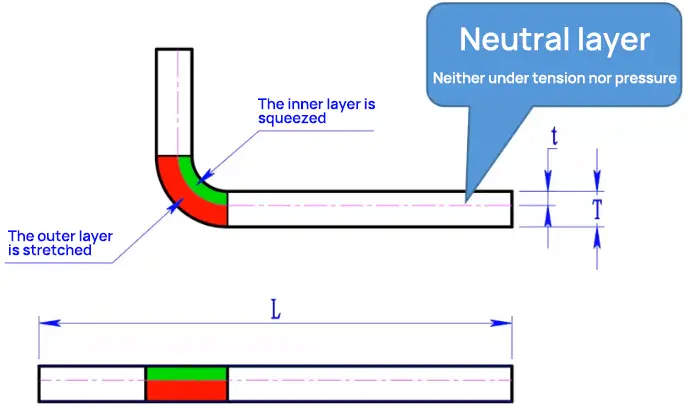
لفهم عامل K بالكامل، من الضروري فهم مفهوم الطبقة المحايدة. عندما يتم ثني جزء من الصفيحة المعدنية، تتعرض المادة القريبة من السطح الداخلي للانحناء للانضغاط، مع زيادة الشدة بالقرب من السطح. وعلى العكس من ذلك، تتعرض المادة القريبة من السطح الخارجي للتمدد، مع زيادة الشدة بالقرب من السطح.
بافتراض أن الصفيحة المعدنية تتكون من طبقات رقيقة متراصة (كما هو الحال مع معظم المعادن)، يجب أن توجد طبقة في المنتصف لا تتعرض للضغط أو التمدد أثناء الثني. تُعرف هذه الطبقة باسم الطبقة المحايدة. تُعد الطبقة المحايدة حاسمة في تحديد عامل K، وبالتالي بدل الانحناء وأبعاد النمط المسطح لجزء الصفيحة المعدنية.
تلعب الطبقة المحايدة، على الرغم من أنها غير مرئية داخل الصفائح المعدنية، دورًا محوريًا في عمليات الثني وترتبط ارتباطًا جوهريًا بخصائص المادة. وتؤثر هذه العلاقة بشكل مباشر على عامل K، وهو معيار حاسم في تصنيع الصفائح المعدنية.
يتم تحديد موضع الطبقة المحايدة من خلال العديد من الخصائص المادية:
وبالتالي، يتأثر عامل K، الذي يمثل موضع الطبقة المحايدة، بخصائص المادة نفسها. ويتم التعبير عنه عادةً في صورة عدد عشري يتراوح بين 0 و1، حيث يشير 0.5 إلى الطبقة المحايدة عند منتصف سماكة الصفيحة.
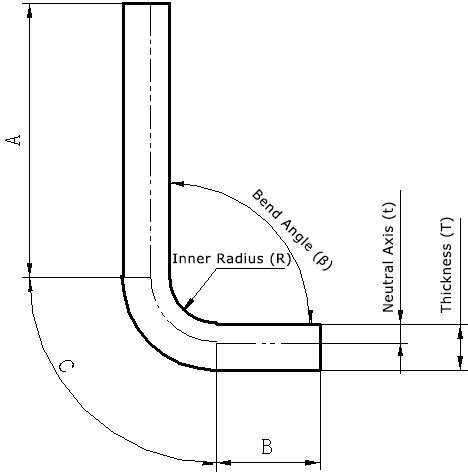
أحد المبادئ الأساسية المستمدة من مفهوم الطبقة المحايدة هو أن الطول غير المطوي (النمط المسطح) لجزء الصفيحة المعدنية المثنية يساوي طول الطبقة المحايدة. ويمكن التعبير عن ذلك رياضياً على النحو التالي:
الطول غير المطوي = الطول المستقيم أ + الطول المستقيم ب + الطول القوسي ج
أين:
هذه العلاقة ضرورية لتحديد أبعاد النمط المسطح بدقة، والتي تعتمد على تحديد عامل K بدقة وحسابات بدل الانحناء. يتأثر بدل الانحناء بدوره بما يلي:
يُمكّن فهم هذه العلاقات المتبادلة المهندسين من:
في الممارسة العملية، بينما توفر الحسابات النظرية نقطة انطلاق، فإن الاختبارات التجريبية وتعديل عوامل K لمجموعات محددة من المواد والأدوات غالبًا ما تسفر عن النتائج الأكثر دقة في بيئات الإنتاج.
تقدم الرسوم التوضيحية أدناه شرحاً مرئياً مفصلاً لمفهوم العامل K:
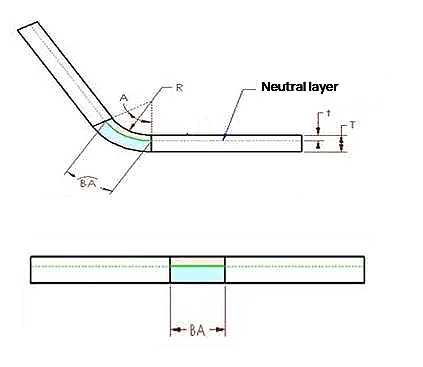
في المقطع العرضي لجزء الصفيحة المعدنية، توجد طبقة أو محور محايد. لا تتعرض المادة الموجودة في هذه الطبقة المحايدة داخل منطقة الانحناء لأي انضغاط أو تمدد، مما يجعلها المنطقة الوحيدة التي تظل غير مشوهة أثناء الانحناء. في الشكل، يتم تمثيل الطبقة المحايدة بتقاطع المنطقتين الوردية (الانضغاط) والزرقاء (التمدد).
تتمثل الفكرة الرئيسية في أنه إذا ظلت الطبقة المحايدة غير مشوهة، يجب أن يكون طول قوس الطبقة المحايدة داخل منطقة الانحناء متساويًا في كل من حالتي الانحناء والتسطيح لجزء الصفيحة المعدنية. يشكل هذا المبدأ الأساس لحساب بدلات الانحناء وأبعاد النمط المسطح باستخدام العامل K.
ولذلك، يجب أن يكون بدل الانحناء (BA) مساويًا لطول قوس الطبقة المحايدة في منطقة الانحناء لجزء الصفيحة المعدنية. ويمثل هذا القوس باللون الأخضر في الشكل.
يعتمد موضع الطبقة المحايدة في الصفائح المعدنية على خواص الموادمثل الليونة.
على افتراض أن المسافة بين طبقة الصفيحة المعدنية المحايدة والسطح "t"، أي العمق من سطح جزء الصفيحة المعدنية إلى الصفيحة مادة معدنية في اتجاه السُمك t.
ولذلك، يمكن التعبير عن نصف قطر قوس طبقة الصفيحة المعدنية المحايدة على الصورة (R+t).
باستخدام هذا التعبير و زاوية الانحناءيمكن التعبير عن طول قوس الطبقة المحايدة (BA) على الصورة
لتبسيط تعريف الطبقة المحايدة في الصفائح المعدنية ومراعاة انطباقها على جميع سماكات المواد، تم إدخال مفهوم العامل k. على وجه التحديد، العامل k هو نسبة سُمك موضع الطبقة المحايدة إلى السُمك الكلي لجزء الصفيحة المعدنية، أي
ولذلك، تكون قيمة K دائمًا بين 0 و1. إذا كانت قيمة العامل K هي 0.25، فهذا يعني أن الطبقة المتعادلة تقع عند 25% من سمك المادة الصفائح المعدنية، وإذا كانت 0.5، فهذا يعني أن الطبقة المتعادلة تقع عند نقطة منتصف سمك المادة بأكملها، وهكذا.
بدمج المعادلتين السابقتين، يمكننا الحصول على المعادلة التالية:
حيث يتم تحديد بعض القيم مثل A وR وT من خلال الشكل الهندسي الفعلي.
ولتحديد قيمة عامل K بدقة، نقدم حاسبتين دقيقتين مصممتين لسيناريوهات إدخال مختلفة. في حين أن النتائج قد تظهر اختلافات طفيفة، فإن كلا الحاسبتين توفران نتائج موثوقة مصممة خصيصًا لمتطلبات تشكيل المعادن الخاصة بك.
الآلة الحاسبة 1: بدل الانحناء المعروف ونصف قطر الانحناء الداخلي
تم تحسين هذه الحاسبة للحالات التي يكون لديك فيها قياسات دقيقة لبدل الانحناء ونصف قطر الانحناء الداخلي. وتستخدم هذه المعلمات لحساب العامل K والمسافة الحرجة من السطح الداخلي إلى المحور المحايد (t)، وهو أمر ضروري لحسابات دقيقة لثني الصفائح المعدنية.
المدخلات:
المخرجات:
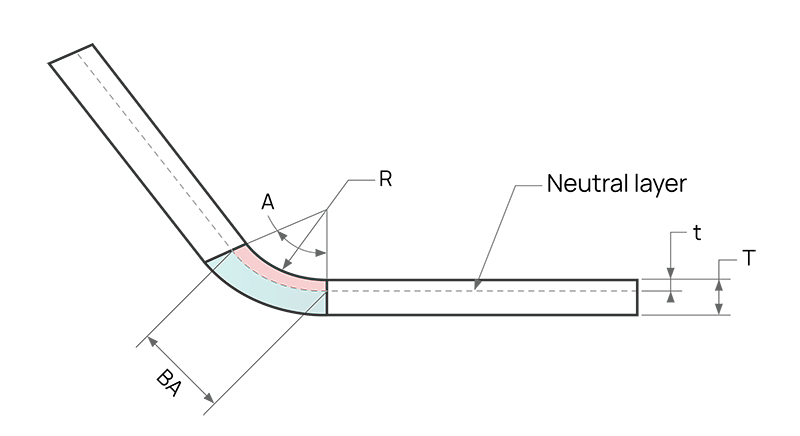
إذا كنت تعرف فقط نصف قطر الانحناء الداخلي وسُمك المادة، فاستخدم هذه الآلة الحاسبة لتحديد عامل K.
المدخلات:
المخرجات:
توفر هذه الآلات الحاسبة طريقة ملائمة لتحديد عامل K وموضع المحور المحايد بسرعة لمشاريع تصميم الصفائح المعدنية الخاصة بك.
بناءً على العمليات الحسابية السابقة، يمكننا استنتاج معادلة حساب عامل K:
أين:
حساب العينة:
دعونا نعمل على نموذج حسابي باستخدام المعلومات المعطاة التالية:
معادلة حساب معامل K هي:
الخطوة 1: عوِّض بالقيم المُعطاة في معادلة عامل K:
K = (2.1 × 180/(3.14 × 90) - 1)/1
الخطوة 2: قم بتبسيط المعادلة:
K ≈ 0.337
ولذلك، بالنسبة إلى المعلمات المعطاة، يكون عامل K هو 0.337 تقريبًا.
يوضح هذا المثال كيفية تطبيق معادلة حساب عامل K لتحديد عامل K لسيناريو ثني صفائح معدنية محددة.
فيما يلي عوامل K للمواد المعدنية الشائعة.
مخطط عامل K
| السُمك (SPCC/SECC) | العامل K (جميع الزوايا، بما في ذلك زاوية R) |
| 0.8 | 0.615 |
| 1 | 0.45 |
| 1.2 | 0.35 |
| 1.5 | 0.348 |
| 2 | 0.455 |
| 3 | 0.349 |
| 4 | 0.296 |
| السُمك (SPCC/SECC) | خصم الانحناء (ينطبق فقط على 90 زاوية 90 درجة) |
| 0.8 | 1 |
| 1 | 1.5 |
| 1.2 | 2 |
| 1.5 | 2.5 |
| 2 | 3 |
| 3 | 5 |
| 4 | 7 |
| 5 | 10 |
يقدم الجدول التالي قيم بدلات الانحناء التي تم الحصول عليها من جهة تصنيع محددة لمختلف المواد والسماكات. يرجى ملاحظة أن هذه القيم هي للإشارة فقط وقد لا تكون قابلة للتطبيق عالمياً.
| سُمك المادة (T) | SPCC | آل | SUS | النحاس |
| 0.8 | 1.4 | 1.4 | 1.5 | – |
| 1.0 | 1.7 | 1.65 | 1.8 | – |
| 1.2 | 1.9 | 1.8 | 2.0 | – |
| 1.5 | 2.5 | 2.4 | 2.6 | – |
| 2.0 | 3.5 | 3.2 | 3.6 | 37 (R3) |
| 2.5 | 4.3 | 3.9 | 4.4 | – |
| 3.0 | 5.1 | 4.7 | 5.4 | 5.0 (R3) |
| 3.5 | 6.0 | 5.4 | 6.0 | |
| 4.0 | 7.0 | 6.2 | 7.2 | 6.9 (R3) |
ملاحظة: بالنسبة للنحاس، قيم بدل الانحناء هي معاملات عندما يكون نصف قطر الانحناء الداخلي R3. عند استخدام المثقاب الحاد للثني، ارجع إلى بدل الانحناء لسبائك الألومنيوم أو حدد القيمة من خلال الثني التجريبي.
لفهم لماذا لا يمكن أن يتجاوز عامل K 0.5، من الضروري فهم مفاهيم عامل K والطبقة المحايدة في ثني الصفائح المعدنية.
ينطوي ثني الصفائح المعدنية على إحداث تشوه محكوم لتشكيل قوس نصف قطر صغير. وعلى عكس التشكيل بالدلفنة، الذي ينتج عنه أنصاف أقطار أكبر، ينتج عن الثني عادةً منحنيات أكثر إحكاماً. وبغض النظر عن طريقة الثني المستخدمة (الثني بالهواء، أو الثني القاعي، أو التشكيل)، فإن تحقيق زاوية قائمة مثالية أمر مستحيل فيزيائياً بسبب خصائص المواد وقيود الأدوات. يرتبط نصف قطر الشُّغْلَة مباشرةً بنصف قطر القالب السفلي - ينتج نصف قطر القالب الأصغر نصف قطر انحناء أكثر إحكامًا، والعكس صحيح.
في عملية ثني الصفائح المعدنية، تخضع المادة لكل من الانضغاط داخل الانحناء والشد من الخارج. ينشئ هذا التشوه مستوى نظريًا داخل سمك المادة حيث لا يحدث أي ضغط أو شد - وهذا ما يُعرف بالطبقة المحايدة أو المحور المحايد.
عند ثني الصفيحة، تنخفض أبعاد السطح الداخلي بينما تزداد أبعاد السطح الخارجي. ينتج عن هذا التغير في الأبعاد بدل الانحناء، وهو عامل حاسم في حسابات الانحناء الدقيقة. على سبيل المثال، عند ثني صفيحة بزاوية 90 درجة من لوح مسطح بأبعاد خارجية 20 × 20 مم، سيكون الطول غير المطوي دائمًا أقل من 40 مم، بغض النظر عن سُمك المادة. ويرجع ذلك إلى استطالة الألياف الخارجية أثناء الثني.
كشفت الأبحاث المتقدمة ومتطلبات التصنيع عالية الدقة أن موضع الطبقة المحايدة لا يكون دائمًا في المركز الدقيق لسُمك المادة. في الواقع، بالنسبة لأنصاف أقطار الانحناءات الصغيرة (عادةً عندما يكون نصف قطر الانحناء الداخلي أقل من ضعف سُمك المادة)، فإن المحور المحايد ينزاح نحو داخل الانحناء.
يحدث هذا التحول لأن قوى الضغط على الجزء الداخلي من الانحناء أكبر من قوى الشد على الجانب الخارجي، مما يؤدي إلى توزيع إجهاد غير متماثل. على سبيل المثال، في الانحناء الضيق، قد ينخفض البُعد الداخلي بمقدار 0.3 مم، بينما يزيد البُعد الخارجي بمقدار 1.7 مم، بدلاً من حدوث تغيرات متساوية بمقدار 1 مم على كلا الجانبين.
عامل K هو معامل بلا أبعاد يُستخدم لتحديد موضع الطبقة المحايدة داخل سُمك المادة أثناء الانحناء. ويُعرَّف بأنه نسبة المسافة من السطح الداخلي للثني إلى الطبقة المحايدة مقسومة على إجمالي سُمك المادة.
رياضيًا، عامل K-factor = d / t، حيث:
d = المسافة من سطح الانحناء الداخلي إلى الطبقة المحايدة
t = السُمك الكلي للمادة
يكون موضع الطبقة المحايدة مقيدًا بالحدود الفيزيائية للمادة. في الحد الأقصى النظري، يمكن أن تقع الطبقة المحايدة عند المركز الدقيق لسمك المادة. في هذه الحالة
د (الحد الأقصى) = t / 2
عامل K-عامل (الحد الأقصى) = (t / 2) / t = 0.5
لذلك، لا يمكن أن يتجاوز عامل K في ثني الصفيحة المعدنية 0.5، لأن هذا يعني أن الطبقة المحايدة تقع خارج الخط المركزي لسمك المادة، وهو أمر مستحيل فيزيائيًا.
في الممارسة العملية، يتراوح عامل K عادةً من 0.3 إلى 0.5، اعتمادًا على خصائص المواد ونصف قطر الانحناء وعملية التشكيل. يعد التحديد الدقيق لعامل K أمرًا بالغ الأهمية لإجراء حسابات دقيقة لبدلات الانحناء وتحقيق تفاوتات أبعاد دقيقة في تصنيع الصفائح المعدنية.
حتى بالنسبة لنفس المادة، فإن عامل K في المعالجة الفعلية ليس ثابتًا ويتأثر بتقنية المعالجة. في مرحلة التشوه المرن لثني الصفائح المعدنية، يقع المحور المحايد في منتصف سُمك اللوحة. ومع ذلك، مع زيادة تشوه الانحناء لقطعة الشغل، تخضع المادة لتشوه بلاستيكي بشكل أساسي، وهو أمر غير قابل للاسترداد.
عند هذه النقطة، تنزاح الطبقة المحايدة نحو الجانب الداخلي من الانحناء مع تغير حالة التشوه. كلما كان التشوه اللدن أكثر شدة، زاد الإزاحة الداخلية للطبقة المحايدة.
لعكس شدة التشوه البلاستيكي أثناء ثني الصفيحة، يمكننا استخدام البارامتر R/T، حيث يمثل R نصف قطر الانحناء الداخلي ويمثل T سُمك الصفيحة. تشير نسبة R/T الأصغر إلى مستوى أعلى من تشوه الصفيحة وانزياح أكبر إلى الداخل للطبقة المحايدة.
يوضح الجدول أدناه بيانات الألواح ذات المقطع العرضي المستطيل في ظل ظروف معالجة محددة. مع زيادة R/T، يزداد أيضًا عامل موضع الطبقة المحايدة K.
| R/T | K |
| 0.1 | 0.21 |
| 0.2 | 0.22 |
| 0.3 | 0.23 |
| 0.4 | 0.24 |
| 0.5 | 0.25 |
| 0.6 | 0.26 |
| 0.7 | 0.27 |
| 0.8 | 0.3 |
| 1 | 0.31 |
| 1.2 | 0.33 |
| 1.5 | 0.36 |
| 2 | 0.37 |
| 2.5 | 0.4 |
| 3 | 0.42 |
| 5 | 0.46 |
| 75 | 0.5 |
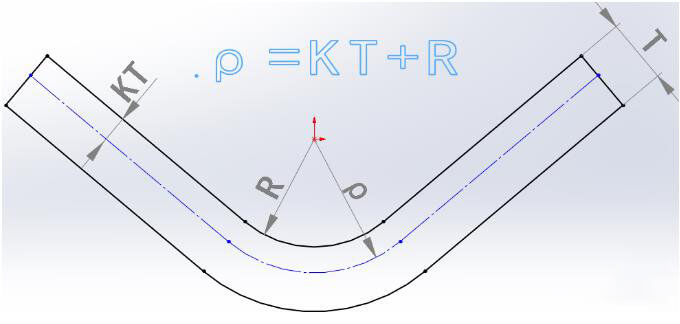
يمكن حساب نصف قطر الطبقة المتعادلة (ρ) باستخدام المعادلة التالية:
ρ = R + KT
أين:
وبمجرد تحديد نصف قطر الطبقة المحايدة، يمكن حساب طولها المطور بناءً على الهندسة، ومن ثم يمكن اشتقاق طول الصفيحة المطورة.
بشكل عام، في ظل ظروف الانحناء نفسها، فإن مواد الصفائح المعدنية الأكثر ليونة لها قيم K أقل وإزاحات داخلية أكبر للطبقة المحايدة.يوفر دليل الماكينات ثلاثة جداول ثني قياسية تنطبق على الانحناء بزاوية 90 درجة، كما هو موضح أدناه:
| الجدول | المواد | العامل K |
| # 1 | النحاس الأصفر الناعم، النحاس | 0.35 |
| # 2 | النحاس الصلب والنحاس والفولاذ الطري والألومنيوم | 0.41 |
| # 3 | النحاس الصلب والبرونز والبارد الصلب المدرفلالفولاذ الزنبركي | 0.45 |
توضح هذه الجداول كيفية تأثير خواص المواد على عامل K وموضع الطبقة المحايدة.
بالنسبة للانحناءات ذات أنصاف الأقطار الداخلية الأصغر، يمكن أن تؤثر زاوية الانحناء أيضًا على التغير في عامل K. كلما زادت زاوية الانحناء، تتعرض الطبقة المحايدة لإزاحة أكبر نحو الجانب الداخلي من الانحناء. هذه العلاقة بين زاوية الانحناء وإزاحة الطبقة المحايدة مهمة بشكل خاص للانحناءات ذات نصف القطر الضيق ويجب أخذها في الاعتبار عند تحديد عامل K المناسب لجزء معين من الصفيحة المعدنية.
في عمليات ثني الصفائح المعدنية، تُعد معايرة عامل K أمرًا بالغ الأهمية لتحقيق نتائج دقيقة ومتسقة. عملية المعايرة هذه ضرورية بسبب عدة عوامل متأصلة في تشكيل المعادن:
من خلال استثمار الوقت في معايرة عامل K، يمكن للمصنعين تحسين دقة حسابات ثني الصفائح المعدنية بشكل كبير، وتحسين جودة المنتج، وتحسين سير العمل من التصميم إلى التصنيع. وعلى الرغم من أن عملية المعايرة هذه تتطلب بعض الجهد في البداية، إلا أنها في النهاية توفر الوقت والموارد من خلال تقليل الأخطاء والتكرارات في عملية تصنيع الصفائح المعدنية.
فيما يلي تحليل شامل لعملية معايرة عامل K لتصميم الصفائح المعدنية في SolidWorks:
من خلال اتباع عملية المعايرة هذه بدقة، فإنك تضمن نمذجة دقيقة للصفائح المعدنية في SolidWorks، مما يؤدي إلى تطوير نمط مسطح دقيق وعمليات تصنيع محسّنة.
لتحديد القيمة المثلى لعامل K لثني الصفائح المعدنية بناءً على خصائص المواد المختلفة، من الضروري فهم دور عامل K وأهميته. عامل K هو قيمة مستقلة تصف كيفية انحناء الصفائح المعدنية وانفتاحها في ظل معلمات هندسية مختلفة. ويُستخدم أيضًا لحساب تعويض الانحناء لمختلف سماكات المواد وأنصاف أقطار الانحناء وزوايا الانحناء. يعد اختيار عامل K المناسب أمرًا حاسمًا لضمان دقة فك وثني أجزاء الصفائح المعدنية.
يمكن تلخيص عملية تحديد القيمة المثلى لعامل K بناءً على خواص المادة في الخطوات التالية:
باتباع هذه الخطوات والنظر في خصائص المواد، والقيم الافتراضية، والتعديلات التجريبية، وجداول خصم الانحناء، ومعلمات الانحناء الإضافية، يمكنك تحديد قيمة عامل K المثلى لتطبيق ثني الصفائح المعدنية المحدد الخاص بك.
س: ما هو النطاق النموذجي لقيم عامل K للمواد الشائعة؟
ج: عادةً ما يتراوح عامل K من 0.3 إلى 0.5، اعتمادًا على خصائص المادة وظروف التشكيل. بالنسبة للمواد اللينة القابلة للسحب مثل النحاس الملدن والألومنيوم، تكون عوامل K أقل عمومًا، حوالي 0.33 إلى 0.38. أما المواد متوسطة القوة مثل الفولاذ الطري والنحاس الأصفر فعادةً ما يكون عامل K بين 0.40 و0.45. تميل المواد عالية القوة مثل الفولاذ المقاوم للصدأ والفولاذ الزنبركي إلى أن يكون لها عوامل K أعلى، تتراوح بين 0.45 و0.50. من المهم ملاحظة أن هذه القيم يمكن أن تختلف بناءً على عوامل مثل سُمك الصفيحة ونصف قطر الانحناء واتجاه الحبيبات.
س: كيف يمكنني اختيار عامل K المناسب لتصميمي للصفائح المعدنية؟
ج: يتضمن اختيار عامل K المناسب مراعاة عوامل متعددة:
تحقق دائمًا من صحة عامل K الذي اخترته من خلال النماذج الأولية أو إنتاج العينات قبل التصنيع على نطاق كامل لضمان الدقة والجودة في الأجزاء النهائية.
في الختام، يُعد العامل K عاملاً حاسمًا في تصميم الصفائح المعدنية وتصنيعها، حيث يعمل كمعامل رئيسي للتنبؤ بدقة بسلوك المواد أثناء عمليات الثني. من خلال فهم علاقته بموضع المحور المحايد وخصائص المواد وظروف التشكيل، يمكن للمصممين والمهندسين إنشاء أنماط مسطحة دقيقة وتحقيق بدلات الانحناء المثلى.
يعد إتقان الفروق الدقيقة في اختيار عامل K وتطبيقه أمرًا ضروريًا لإنتاج أجزاء صفائح معدنية عالية الجودة بدقة أبعاد وأداء متناسق. مع استمرار تطور تقنيات التصنيع والمواد، سيظل البقاء على اطلاع على أحدث الأبحاث وأفضل الممارسات الصناعية فيما يتعلق بتحديد عامل K أمرًا بالغ الأهمية للحفاظ على الميزة التنافسية في تصنيع الصفائح المعدنية.
مزيد من القراءة والمصادر
لتعميق فهمك لمفهوم ثني الصفائح المعدنية والمفاهيم ذات الصلة، استكشف الموارد التالية:
بصفتي مؤسس شركة MachineMFG، فقد كرّستُ أكثر من عقد من حياتي المهنية في مجال تصنيع المعادن. وقد أتاحت لي خبرتي الواسعة أن أصبح خبيرًا في مجالات تصنيع الصفائح المعدنية، والتصنيع الآلي، والهندسة الميكانيكية، وأدوات الماكينات للمعادن. أفكر وأقرأ وأكتب باستمرار في هذه المواضيع، وأسعى باستمرار للبقاء في طليعة مجال عملي. فلتكن معرفتي وخبرتي مصدر قوة لعملك.
AR 
EN 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO