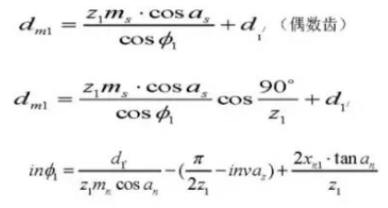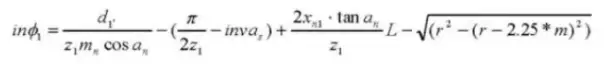
Вы когда-нибудь задумывались об увлекательном мире шестеренок? В этой статье блога мы рассмотрим историю, типы и терминологию этих важнейших механических компонентов. Присоединяйтесь к нам, поскольку мы погрузимся в тонкости зубчатых передач, руководствуясь опытом опытного инженера-механика. Узнайте, как шестеренки развивались на протяжении веков, и познакомьтесь с их важнейшей ролью в современном оборудовании.
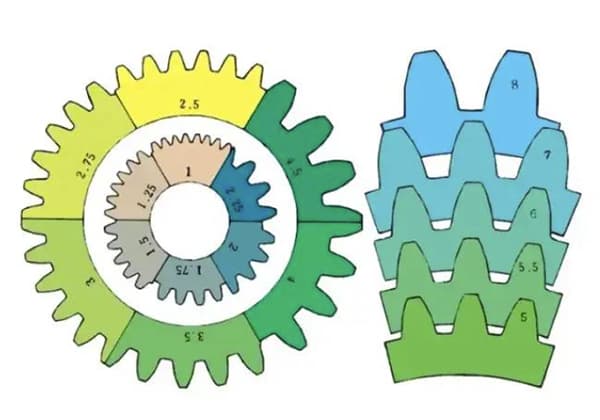
Шестерня - это прецизионный зубчатый механический компонент, предназначенный для зацепления с другими шестернями или зубчатыми компонентами. Она является основополагающим элементом в системах передачи энергии, преобразуя скорость вращения и крутящий момент между валами. Шестерни характеризуются круглой формой с равномерно расположенными зубьями по периферии, которые обычно имеют эвольвентный профиль для оптимального зацепления.
Применение зубчатых передач в механической трансмиссии и в других отраслях машиностроения чрезвычайно разнообразно и важно. Они являются неотъемлемой частью широкого спектра машин и устройств, от простых ручных инструментов до сложного промышленного оборудования и высокопроизводительных автомобилей. Шестерни обеспечивают точный контроль скорости, направления и силы в механических системах, что делает их незаменимыми в силовых передачах, редукторах, дифференциалах и множестве других механических узлов.
Универсальность зубчатых передач обусловлена их способностью изготавливаться в различных размерах, материалах и конфигурациях, включая прямозубые, косозубые, конические и червячные передачи, каждая из которых подходит для конкретных применений и требований к производительности. По мере развития технологий конструкция и производство зубчатых колес продолжают совершенствоваться, в них внедряются новые материалы, технологии производства и методы оптимизации для повышения эффективности, долговечности и снижения уровня шума в механических системах.
Еще в 350 году до нашей эры знаменитый древнегреческий философ Аристотель писал о шестеренках в своей литературе.
Около 250 года до н. э. математик Архимед в своей литературе также описал использование турбины и червячной передачи в подъемном механизме.
В водяных часах Ктесибиоса в Ираке до сих пор сохранились шестеренки, сделанные за много веков до нашей эры.
История зубчатых колес в Китае уходит корнями в глубокую древность и имеет долгую и обширную историю. Согласно историческим записям, уже в 400-200 годах до нашей эры в Древнем Китае использовались зубчатые колеса.
Бронзовые шестеренки, раскопанные в провинции Шаньси, - самые древние шестеренки, обнаруженные до сих пор в мире. Управляемые вагонетки, отражающие достижения древней науки и техники, представляли собой механические устройства, вращающиеся вокруг зубчатых механизмов.
В эпоху итальянского Возрождения во второй половине XV века знаменитый гений Леонардо да Винчи не только оставил неизгладимый след в культуре и искусстве, но и внес значительный вклад в историю зубчатых технологий.
Спустя более 500 лет современные шестеренки все еще хранят эскизы прототипов того времени.
(1) цилиндрическая шестерня
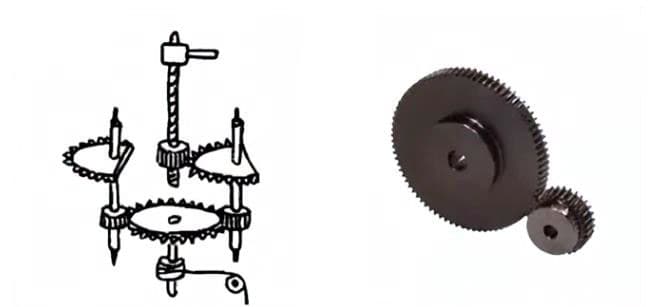
(2) Реечная шестерня
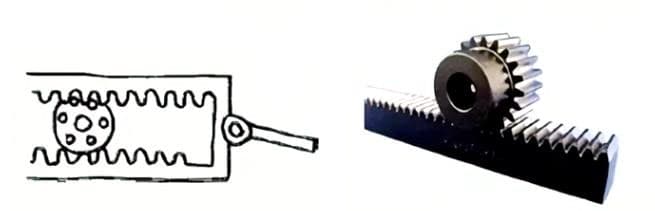
(3) Цилиндрическая передача со скрещенными осями
(4) Коническая шестерня
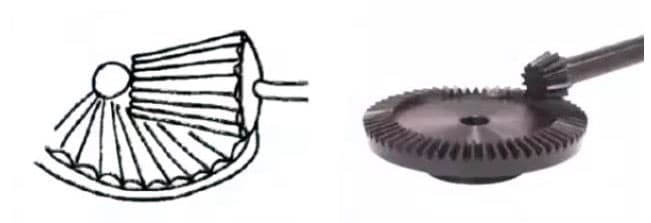
(5) Гипоидная коническая передача с высоким передаточным отношением
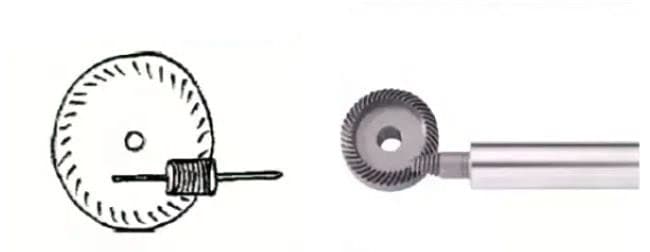
(6) Червячная передача
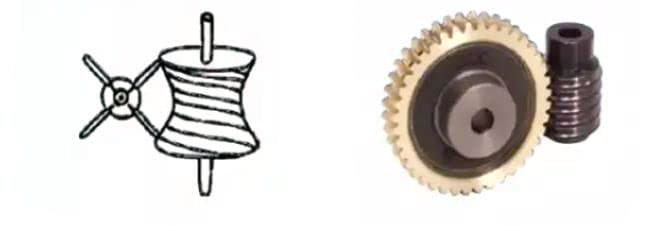
Только в конце XVII века люди начали изучать форму зубьев колеса, которые могли точно передавать движение. После промышленной революции в Европе в XVIII веке применение зубчатой передачи стало все более широким.
Сначала была разработана циклоидальная передача, затем эвольвентная. К началу XX века эвольвентная передача стала доминирующей в своем применении. Позже были разработаны такие передачи, как косозубая, дуговая, коническая и косоугольная.
Сегодня современные технологии производства зубчатых колес достигли больших успехов. Модули зубчатых колес варьируются от 0,004 до 100 миллиметров, диаметр шестерни может составлять от 1 миллиметра до 150 метров. На сайте передача энергии Мощность может достигать 100 000 киловатт, а скорость вращения - 100 000 оборотов в минуту. Наибольшая окружная скорость может достигать 300 метров в секунду.
В мире редукторы для силовых передач развиваются в направлении миниатюризации, высокой скорости и стандартизации. Некоторые тенденции в проектировании редукторов включают применение специальных зубчатых колес, разработку планетарных редукторов, а также исследование и разработку систем редукторов с низким уровнем вибрации и шума.
Существуют различные типы зубчатых передач, и наиболее распространенный метод классификации основан на оси передачи.
Как правило, зубчатые передачи делятся на три типа: с параллельными осями, с пересекающимися осями и с перекошенными осями.
Параллельно-осевые шестерни: включая цилиндрические и косозубые шестерни, внутренние зубчатые колеса, стойки и косозубые стойки.
IПередачи с пересекающимися осями: В том числе прямые конические шестерни, спиральные конические шестерни, конические шестерни с нулевым градусом и т.д.
Косозубые шестерни: включая косозубые передачи со скрещивающимися осями, червячные передачи, гипоидные конические передачи и т.д.
| Тип зубчатой передачи | Тип передачи | Эффективность передачи (%) | Трехмерное графическое представление |
Параллельно-осевой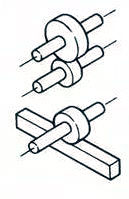 | Прямозубые шестерни | 98.0-99.5 |  |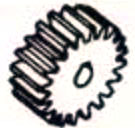
| Косозубые шестерни |  | ||
| Стойки, спиральные стойки |  | ||
| Внутримассовые передачи |  | ||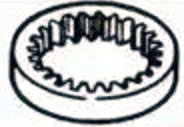
Пересекающаяся ось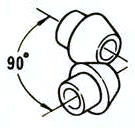 | Пильные шестерни | 98.0-99.0 |  |
| Прямые конические шестерни |  | ||
| Спирально-конические шестерни |  | ||
Ось перекоса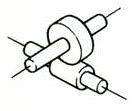 | Винтовые передачи | 70.0-95.0 |  |
| Черви | 30.0-90.0 |  | |
| Червячные колеса |  |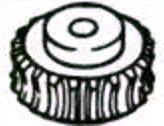
КПД, указанный в таблице выше, - это КПД передачи, который не включает потери на подшипники и смазку при перемешивании. Зацепление параллельно-осевых и пересекающихся пар зубчатых колес происходит в основном за счет качения, и относительное скольжение очень мало, поэтому КПД высокий.
Зацепление пар ступенчато-осевых зубчатых колес, таких как косозубые и червячные, оказывает значительное влияние на трение, поскольку передача мощности осуществляется за счет относительного скольжения, что приводит к снижению эффективности передачи по сравнению с другими зубчатыми колесами.
КПД зубчатых передач означает эффективность передачи в нормальном монтажном состоянии.
При неправильной установке, особенно когда расстояние между коническими шестернями в сборе неверно и вызывает ошибку при пересечении одной и той же конической шестерни, ее эффективность значительно снизится.
1. Шестерни
Цилиндрические шестерни, у которых линии зубьев и осевые линии параллельны. Они широко используются в силовых передачах, так как легко поддаются обработке.
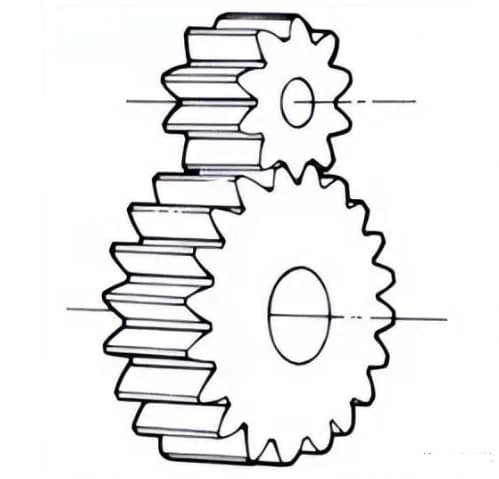
2. Стойка
Прямозубая шестерня, входящая в зацепление с цилиндрическими шестернями. Ее можно рассматривать как частный случай, когда диаметр шага прямозубой шестерни становится бесконечно большим.
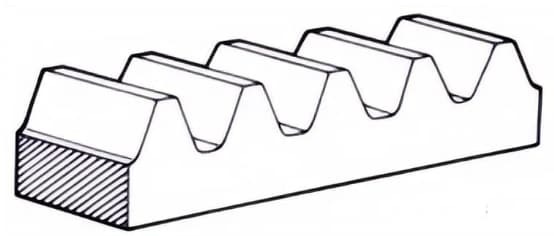
3. Внутренние шестерни
Шестерни с зубьями, обработанными на внутренней стороне кольца, которые входят в зацепление с цилиндрическими шестернями. В основном они используются в таких областях, как планетарные механизмы передачи и зубчатые муфты.
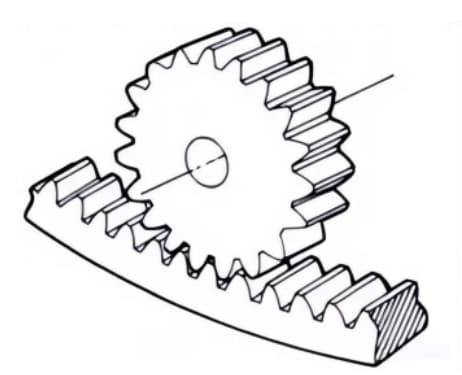
4. Цилиндрические шестерни
Цилиндрические шестерни с линиями зубьев в виде спирали. Они широко используются благодаря высокой прочности и плавности хода по сравнению с прямозубыми шестернями. При передаче они создают осевое усилие.
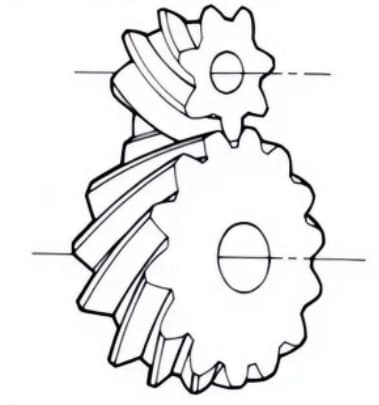
5. Спиральная стойка
Реечная передача, входящая в зацепление с косозубыми шестернями. Это эквивалентно случаю, когда диаметр шага косозубой шестерни становится бесконечно большим.
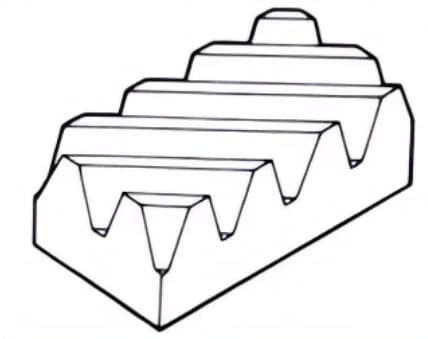
6. Елочные шестеренки
Передачи, состоящие из двух косозубых шестерен с противоположными углами наклона спирали. Их преимущество в том, что они не создают осевой тяги.
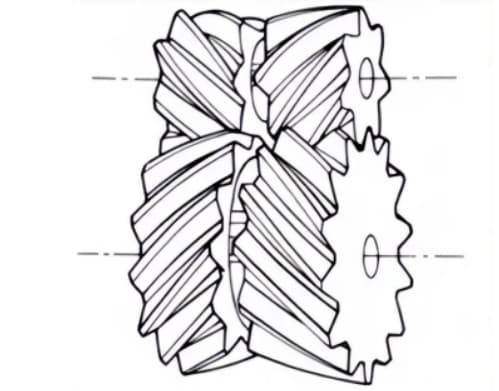
1. Прямые конические шестерни
Конические шестерни с линиями зубьев, параллельными генераторной матрице конуса. Они относительно просты в изготовлении по сравнению с другими типами конических передач.
Поэтому они широко используются в конических передачах для передачи энергии.
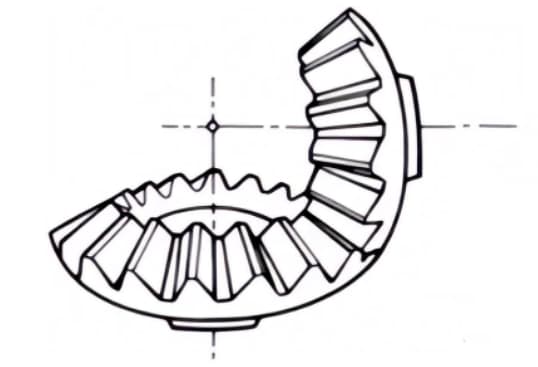
2. Спиральные конические шестерни
Конические шестерни с изогнутыми зубьями и углом спирали. Хотя они сложнее в изготовлении, чем прямые конические шестерни, они широко используются в качестве высокопрочных и малошумных передач.
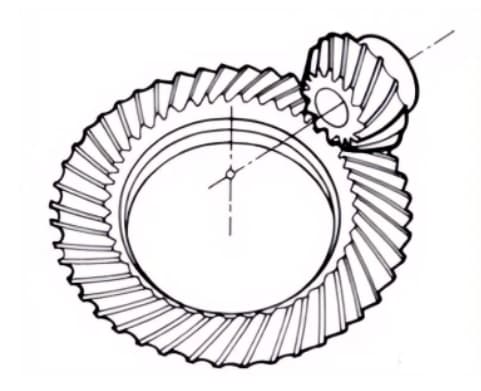
3. Нулевые конические шестерни
Изогнутые конические шестерни с углом спирали ноль градусов. Они обладают характеристиками как прямых, так и спиральных конических передач, при этом поверхность зубьев подвергается тем же силовым воздействиям, что и у прямых конических передач.
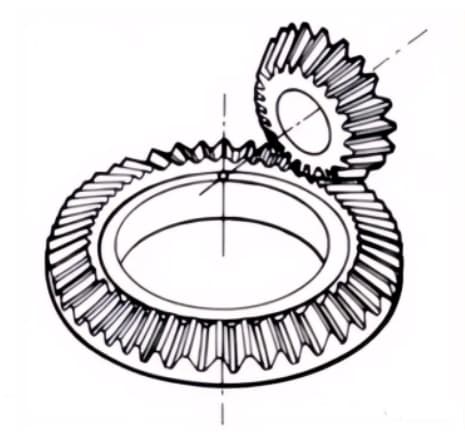
1. Пара червячных шестерен
Под термином "червячная пара" понимается комбинация червяка и входящего в зацепление с ним червячного колеса. Главная особенность червячной пары заключается в том, что с помощью одной пары можно получить большое передаточное отношение, и они работают бесшумно. Однако их низкий КПД является недостатком.
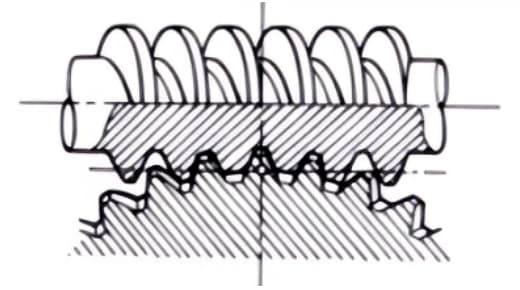
2. Пара косозубых и червячных шестерен
Термин, используемый, когда цилиндрические червячные пары используются для передачи между ступенчатыми осями. Они могут использоваться в паре с цилиндрическими шестернями или между цилиндрическими и прямозубыми шестернями. Хотя они работают плавно, их можно использовать только при небольших нагрузках.
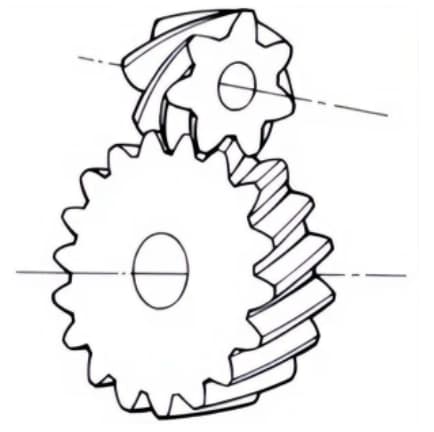
1. Торцевые шестерни
Дискообразные шестерни, которые могут входить в зацепление с прямозубыми или косозубыми шестернями. Они используются для передачи между ортогональными и ступенчатыми осями.
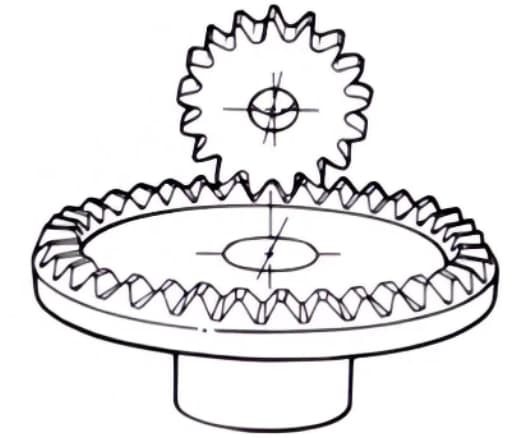
2. Пара червячных шестерен с песочными часами
Под термином "червячная зубчатая пара" понимается комбинация червяка с песочными часами и червячного колеса, входящего с ним в зацепление. Хотя они сложнее в изготовлении по сравнению с цилиндрическими червячными парами, они могут передавать большие нагрузки.
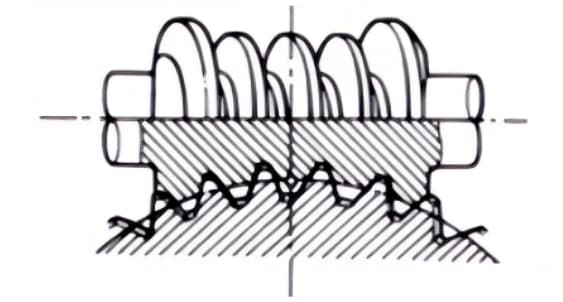
3. Гипоидные шестерни
Конические шестерни, используемые для передачи сигнала между ступенчатыми осями. Большая и меньшая шестерни обрабатываются эксцентрично, как и в случае со спиральными коническими шестернями. Принцип зацепления очень сложный.
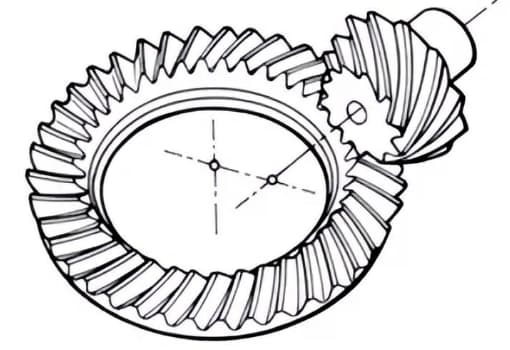
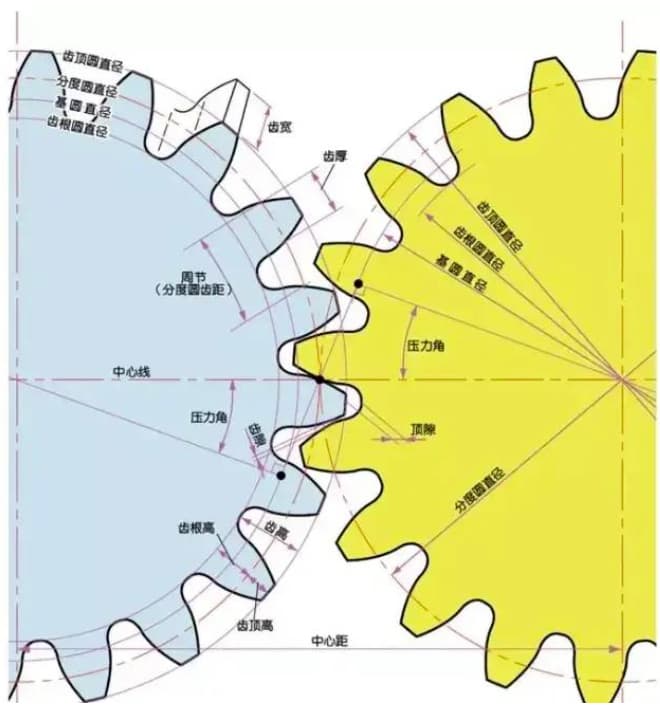
У зубчатых передач есть своя терминология и способы представления. Для того чтобы лучше понять суть зубчатых передач, приведем некоторые часто используемые основные термины зубчатых передач.
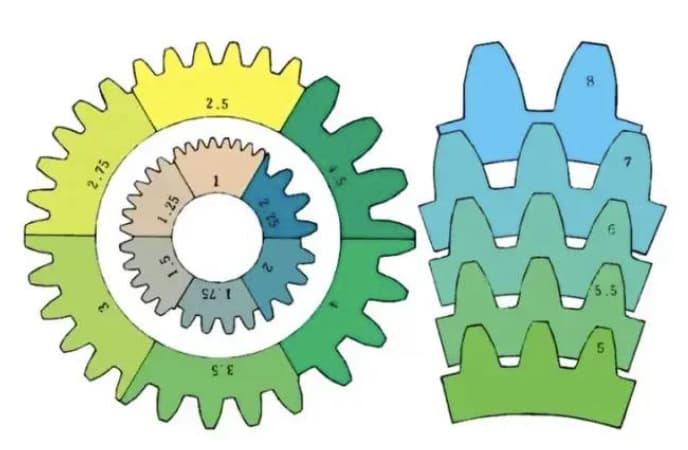
m1, m3, m8... известны как модуль 1, модуль 3, модуль 8 соответственно. Модуль повсеместно используется во всем мире для обозначения размера шестерни, используя символ m (модуль) и цифры (миллиметры) для обозначения размера зубьев.
Чем больше число, тем больше передача.
В странах, использующих имперские единицы измерения, таких как США, размер зубьев обозначается символом DP (диаметральный шаг) и цифрами (количество зубьев для шестерни с диаметром шага 1 дюйм).
Например: DP24, DP8 и т. д. Существует также сравнительный и специальный метод обозначения размера зубьев с помощью символа CP (круговой шаг) и цифр (миллиметров), например, CP5, CP10.
Шаг (p) можно получить, умножив модуль на pi. Шаг - это длина между соседними зубьями.
Формула: p= pi x m
Сравнение размеров зубцов для разных модулей:
Угол давления - это параметр, определяющий форму зубьев шестерни. Он обозначает наклон поверхности зубьев шестерни и обычно устанавливается на уровне 20 градусов (α).
Ранее были распространены передачи с углом давления 14,5 градусов.
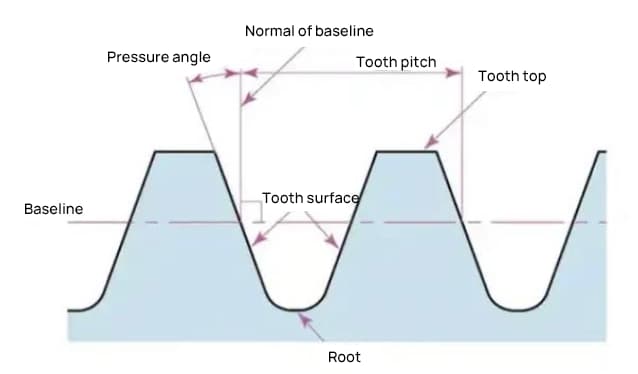
Угол давления - это угол, образованный между радиусом и касательной к форме зуба в определенной точке на поверхности зуба (обычно в узле). Как показано на рисунке, α - это угол давления. α' также является углом давления, так как α' = α.
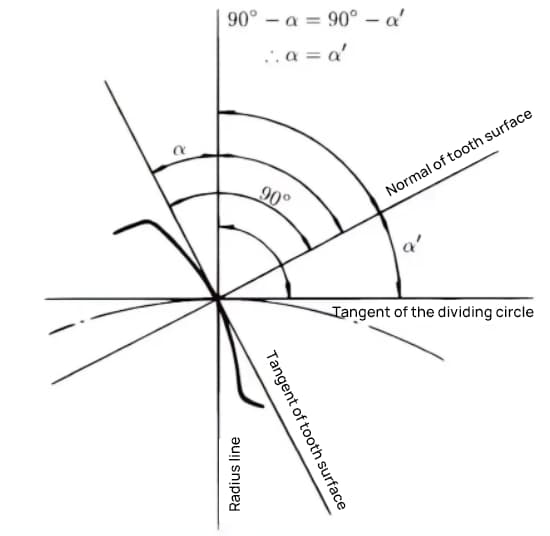
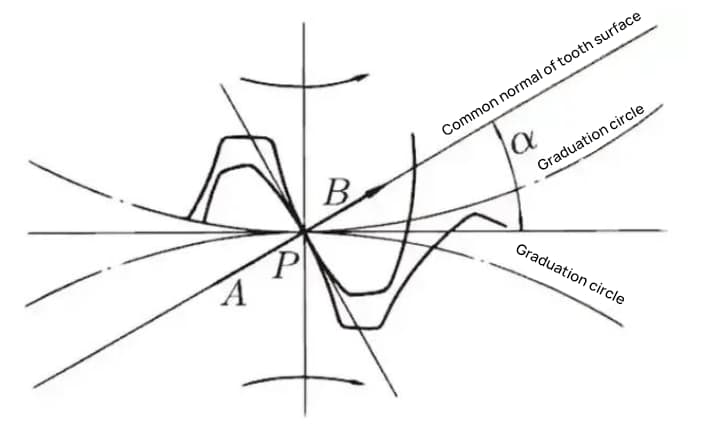
Когда состояние зацепления шестерни A и шестерни B рассматривается из узла, шестерня A толкает шестерню B из узла. В это время движущая сила действует на общую нормаль шестерни A и шестерни B. Другими словами, общая нормаль - это направление силы и направление давления, а α - угол давления.
Модуль (m), угол давления (α) и число зубьев (z) - три основных параметра зубчатого колеса. Исходя из них, каждая часть шестерни рассчитывается по размерам.
Высота зуба шестерни определяется модулем (m).
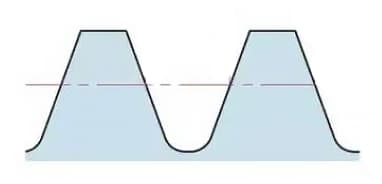
Полная высота зуба составляет h=2,25 м (= высота сложения + высота вычитания).
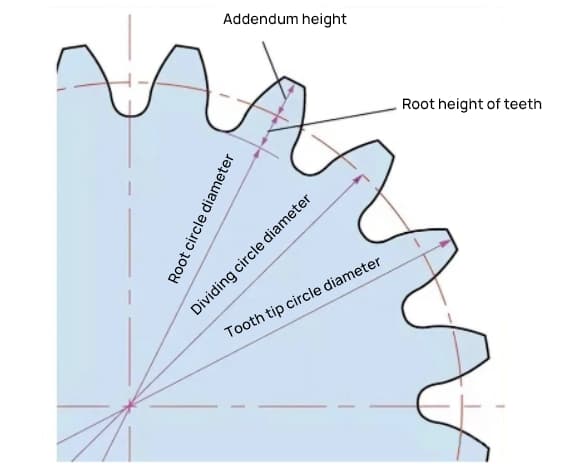
Высота сложения (ha) - это высота от вершины зуба шестерни до делительной окружности. ha=1м.
Высота вычета (hf) - это высота от корня зуба шестерни до делительной окружности. hf=1,25 м.
Толщина зуба шестерни (s) равна половине шага. s=πm/2.
Параметром, определяющим размер шестерни, является диаметр ее делительной окружности (d). На основе делительной окружности можно определить шаг, толщину, высоту, высоту сложения и высоту вычитания шестерни.
Диаметр делительной окружности равен d=zm.
Диаметр добавочной окружности равен da=d+2m.
Диаметр окружности дедендума равен df=d-2,5 м.
Окружность шага не видна непосредственно на самом зубчатом колесе, поскольку это предполагаемая окружность, используемая для определения размера зубчатого колеса.
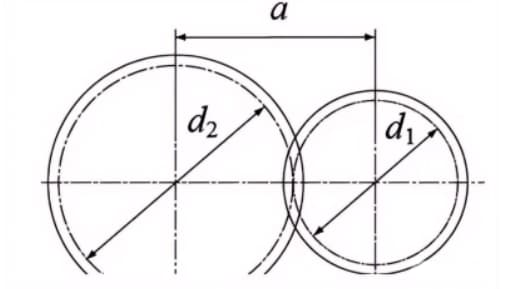
Когда делительные окружности пары шестерен входят в зацепление по касательной, то центральное расстояние равна половине суммы диаметров делительных окружностей.
Расстояние между центрами a=(d1+d2)/2
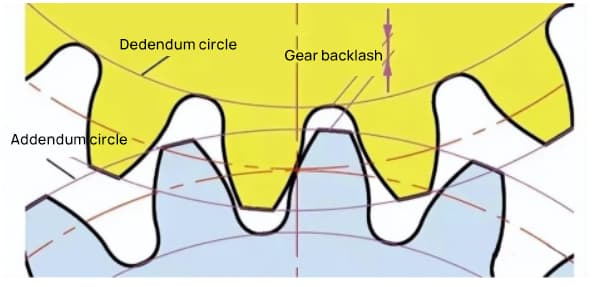
Люфт - важный фактор, обеспечивающий плавное зацепление зубчатых колес. Это пространство между поверхностями зубьев, когда пара шестерен находится в зацеплении.
Существует также зазор в направлении высоты зуба шестерни. Этот зазор называется осевым зазором или зазором (c). Зазор (c) - это разница между диаметром корневой окружности шестерни и диаметром вершины окружности ее сопряженной шестерни.
Зазор c=1.25m-1m=0.25m
Передача, зубья которой закручиваются по спирали вслед за цилиндрической, называется косозубой. Большинство геометрических расчетов для прямозубых передач применимы и к косозубым. Существует два типа косозубых передач, основанных на их опорных поверхностях:
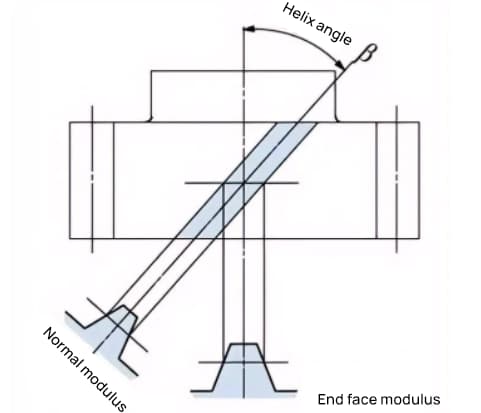
Для косозубых передач, таких как косозубые и циклоидальные, зубья которых имеют спиралевидную форму, направление спирали и зацепление фиксированы.
Направление спирали означает, что ось шестерни направлена вверх или вниз, направление зубьев - верхнее правое, а верхнее левое - левое, если смотреть спереди. Ниже показано зацепление различных типов зубчатых колес.
Если зубья с одинаковым расстоянием между ними разделены только по внешней периферии фрикционного колеса, снабжены выступами, а затем входят в зацепление и вращаются друг с другом, могут возникнуть следующие проблемы:
Когда передача должна быть одновременно тихой и плавной, используются эвольвентные кривые.
Эвольвентная кривая - это кривая, полученная путем наматывания проволоки с карандашом на внешнюю периферию цилиндра и постепенного отпускания проволоки в напряженном состоянии.
Кривая, проведенная карандашом, - это эвольвентная кривая, а внешняя периферия цилиндра называется базовой окружностью.
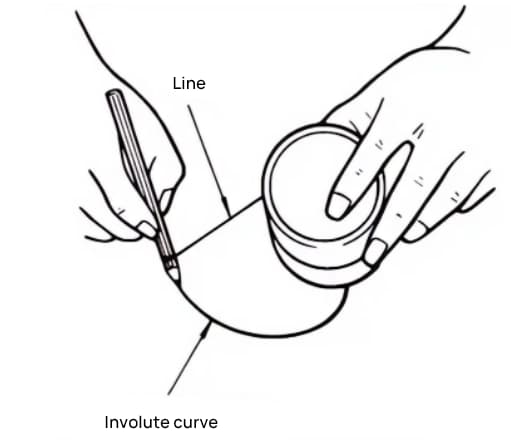
Разделите цилиндр на 8 равных частей и привяжите к ним 8 карандашей, чтобы нарисовать 8 эвольвентных кривых. Затем намотайте проволоку в противоположном направлении и нарисуйте еще 8 кривых тем же методом. Это 8-зубая шестерня с эвольвентными кривыми в качестве профиля зубьев.
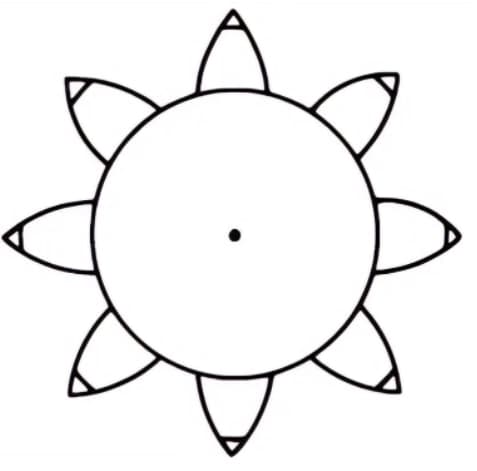
К преимуществам эвольвентных передач относятся способность передавать постоянное отношение скоростей, плавность работы за счет постепенно меняющейся формы контакта и низкая чувствительность к изменению межосевого расстояния.
Базовая окружность - это основная окружность, которая формирует эвольвентный профиль зуба. Окружность шага - это опорная окружность, определяющая размер шестерни. Окружность основания и окружность шага - важные геометрические размеры зубчатых колес.
Эвольвентный профиль зуба представляет собой кривую, образованную на внешней стороне базовой окружности, а угол давления на базовую окружность равен нулю.
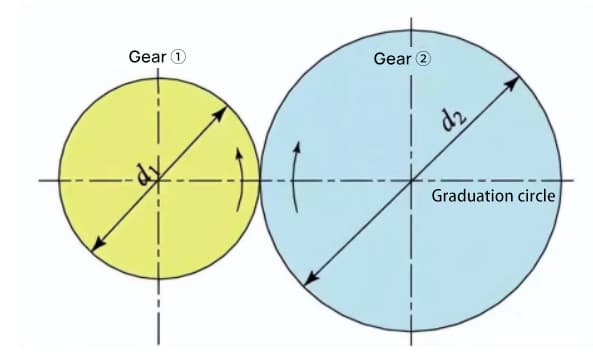
При зацеплении двух стандартных эвольвентных зубчатых колес их делительные окружности проходят по касательной друг к другу на стандартном межцентровом расстоянии. Внешне зацепление двух шестерен выглядит как передача двух фрикционных колес с диаметрами d1 и d2 соответственно.
Однако зацепление эвольвентных зубчатых колес зависит от базовой окружности, а не от делительной окружности.
Точки контакта между зацепляющимися зубьями двух шестерен перемещаются вдоль линии действия в последовательности P1, P2 и P3.
Обратите внимание на желтый зуб шестерни в ведущей шестерне. После того как этот зуб входит в зацепление, шестерня на некоторое время оказывается в состоянии зацепления двух зубьев (P1, P3). Зацепление продолжается, и когда точка контакта перемещается в точку P2 на делительной окружности, в зацеплении остается только один зуб.
Зацепление продолжается, и когда точка контакта перемещается в точку P3, следующий зуб шестерни начинает зацепляться с точкой P1, снова образуя двухзубое зацепление. Таким образом, двухзубое зацепление и однозубое зацепление шестерен взаимодействуют и многократно передают вращательное движение.
Общая касательная линия между базовыми окружностями A-B называется линией действия. Все точки соприкосновения зубчатых пар находятся на этой линии действия.
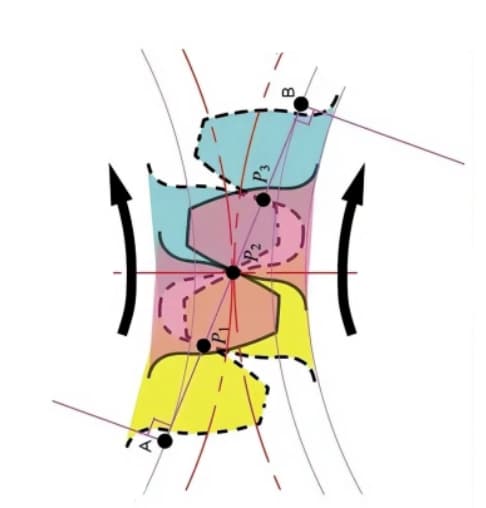
На наглядной схеме это выглядит как ремень, проходящий по внешним перифериям двух базовых окружностей и передающий энергию посредством вращательного движения.
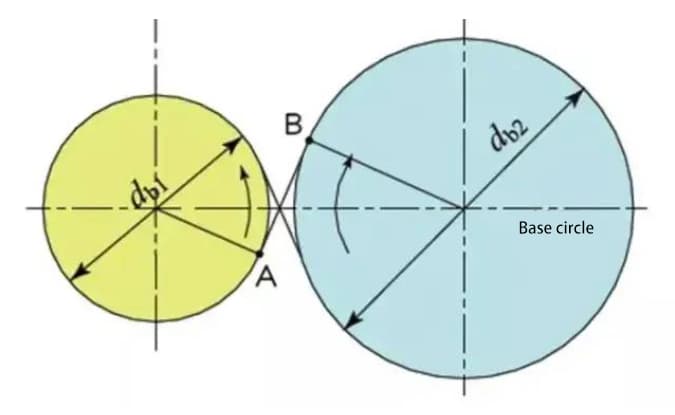
Профиль зубьев шестерен, которые мы обычно используем, как правило, стандартный эвольвентный, но бывают ситуации, когда зубья шестерен необходимо сместить, например, чтобы отрегулировать межосевое расстояние или предотвратить подрезание меньшей шестерни.
Эвольвентная кривая формы зуба зависит от количества зубьев. Чем больше зубьев, тем больше кривая формы зуба стремится к прямой линии.
С увеличением количества зубьев форма корня зуба становится толще, и прочность зубчатого колеса возрастает.
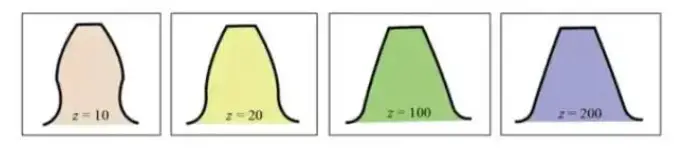
Из приведенного выше графика видно, что для шестерни с 10 зубьями часть эвольвентного профиля у корня зуба удаляется, что приводит к подрезанию.
Однако, приняв положительное смещение для шестерни с z=10, увеличив диаметр добавочной окружности и увеличив толщину зубьев шестерни, можно добиться такой же прочности шестерни, как и у шестерни с 200 зубьями.
На следующем рисунке показана схема 10-зубой передачи с принудительным перемещением. При зубофрезеровании величина перемещения инструмента в радиальном направлении называется величиной радиального смещения (далее - величина смещения) xm(мм).
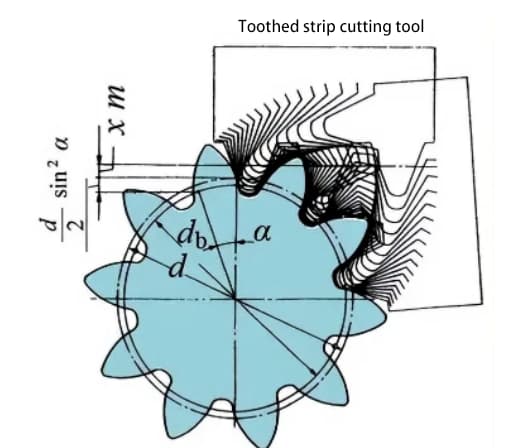
За счет положительного смещения профиля зуба увеличивается толщина зуба шестерни, а также внешний диаметр (диаметр добавочной окружности).
Использование принудительного смещения позволяет избежать подрезания шестерен. Смещение зубчатых колес также может использоваться для других целей, например, для изменения межосевого расстояния. Положительное смещение может увеличить межосевое расстояние, а отрицательное - уменьшить.
Независимо от того, является ли это передача с положительным или отрицательным смещением, существуют ограничения на величину смещения.
Смещение может быть положительным или отрицательным. Хотя высота зуба одинакова, толщина зуба различна. Шестерня с увеличенной толщиной зуба - это шестерня с положительным смещением, а шестерня с уменьшенной толщиной зуба - шестерня с отрицательным смещением.
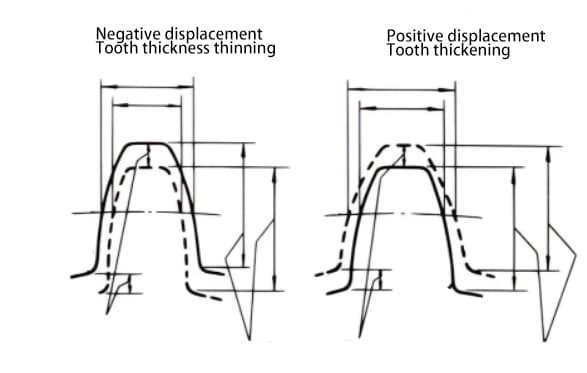
Если невозможно изменить межосевое расстояние между двумя шестернями, можно применить положительное смещение для меньшей шестерни (чтобы избежать подрезания) и отрицательное смещение для большей шестерни, чтобы добиться одинакового межосевого расстояния. В этом случае абсолютное значение величины смещения равно.
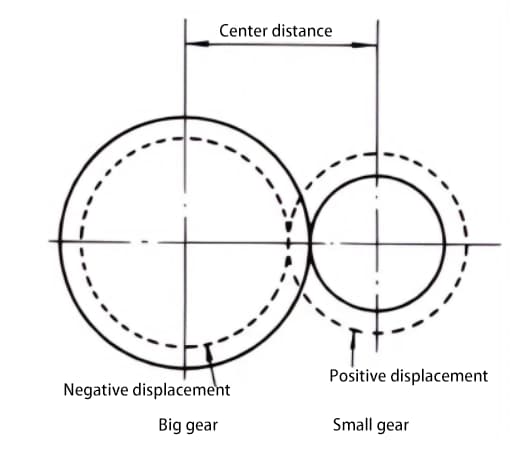
Стандартные шестерни входят в зацепление, когда их делительные окружности касательны друг к другу. Зацепление смещенных шестерен, как показано на рисунке, происходит по касательной к окружности зацепления.
Угол давления на окружности зацепления называется углом зацепления. Угол зацепления отличается от угла давления на делительной окружности (угол давления на делительной окружности) и является важным фактором при проектировании смещенных зубчатых колес.
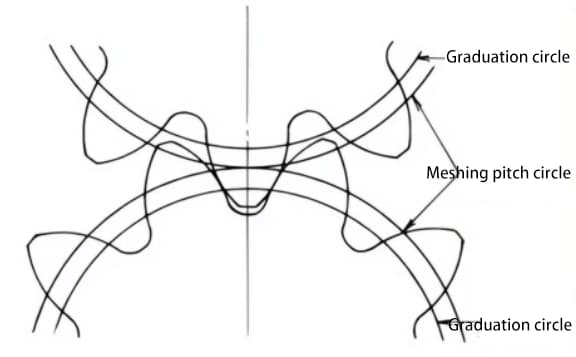
Смещение зубчатых колес позволяет предотвратить подрезание, вызванное малым числом зубьев при обработке. Необходимое межосевое расстояние может быть получено за счет смещения.
В паре зубчатых колес с большой разницей в количестве зубьев положительное смещение может быть приложено к легко изнашиваемой меньшей шестерне, чтобы увеличить толщину зубьев, а отрицательное смещение может быть приложено к большей шестерне, чтобы уменьшить толщину зубьев, чтобы сделать срок службы двух шестерен более сопоставимым.
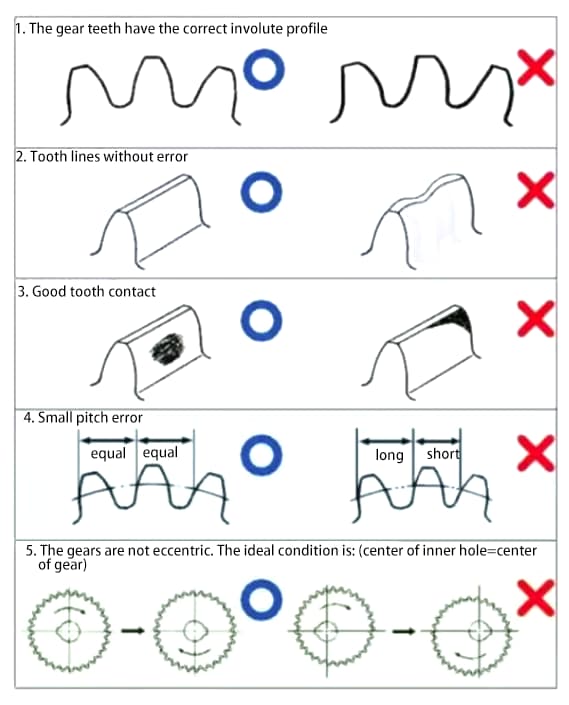
Шестерни - это механические компоненты, передающие энергию и вращение. Основными требованиями к работе шестерен являются:
Для того чтобы соответствовать вышеуказанным требованиям, повышение точности зубчатых колес становится необходимой задачей.
Точность зубчатых колес можно условно разделить на три категории:
a) Точность эвольвентного профиля зуба - точность профиля зуба
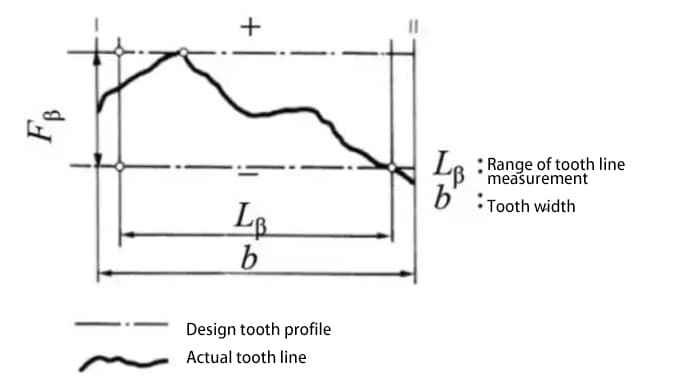
b) Точность боковой линии зуба на поверхности зуба - точность линии зуба
c) Точность положения зубьев/пазов.
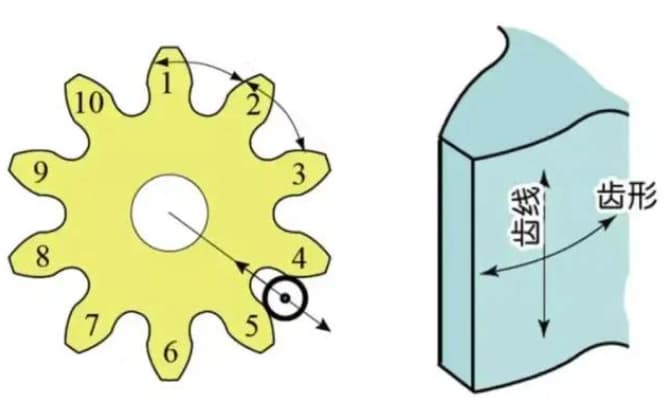
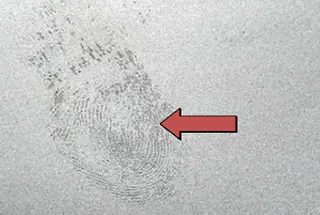
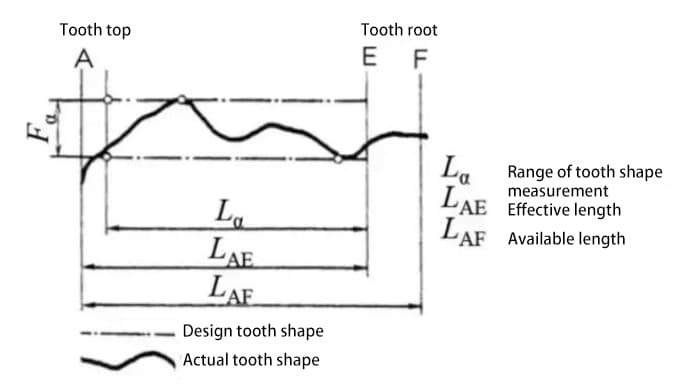
Погрешность профиля зуба - это погрешность между фактическим профилем зуба шестерни и теоретическим профилем зуба.
На погрешность профиля зуба влияет множество факторов, таких как инструмент и вибрации станка в процессе резания.
Погрешность профиля зуба влияет на характеристики зацепления и шум. Поэтому необходимо контролировать погрешность профиля зуба в допустимых пределах.
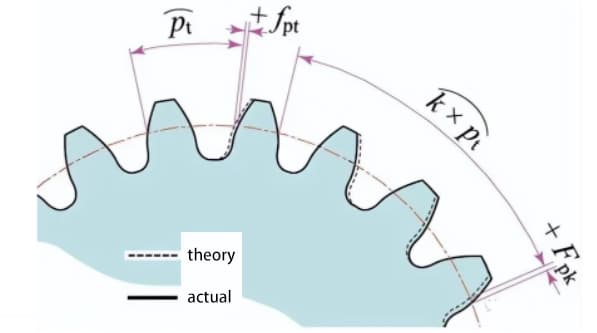
Измерьте величину шага на измерительной окружности, расположенной по центру вала шестерни.
Отклонение шага одного зуба (fpt) - это разница между фактическим и теоретическим шагом.
Общее суммарное отклонение шага (Fp) используется для оценки отклонения шага всей передачи. Общее амплитудное значение кривой суммарного отклонения шага представляет собой общее отклонение шага.
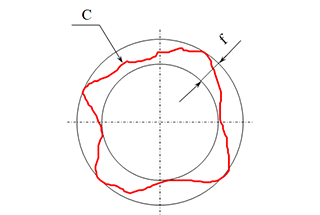
Последовательно поместите зонд (сферический или цилиндрический) в паз зубьев и измерьте разницу между максимальным и минимальным радиальными расстояниями от зонда до оси шестерни. Эксцентриситет вала шестерни - один из факторов, способствующих возникновению радиального биения.
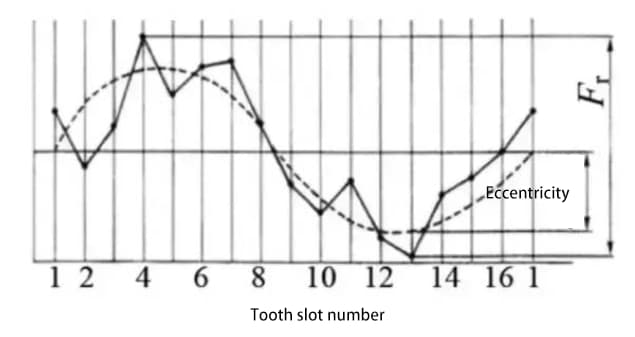
До сих пор описанные нами методы оценки точности зубчатых колес, такие как форма зуба, шаг и точность боковой поверхности зуба, - все это методы оценки точности отдельного зубчатого колеса.
Напротив, существует другой метод, который оценивает точность зубчатых колес путем проведения испытания на зацепление двух зубьев в сочетании с измерительной шестерней. Две поверхности испытуемой шестерни входят в зацепление с измерительной шестерней и вращаются в течение всего цикла. Изменение межосевого расстояния регистрируется.
На рисунке ниже показаны результаты испытаний для шестерни с 30 зубьями. Для радиального композитного отклонения одного зуба имеется в общей сложности 30 волновых линий.
Значение радиального композитного отклонения приблизительно равно сумме радиального отклонения от биения и радиального композитного отклонения одного зуба.
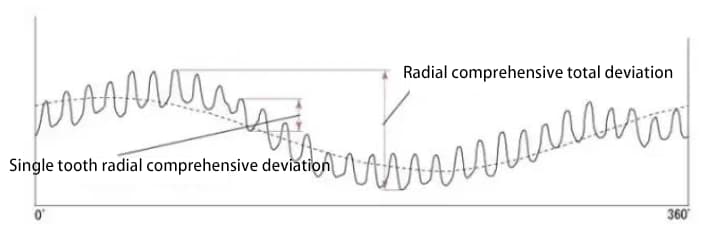
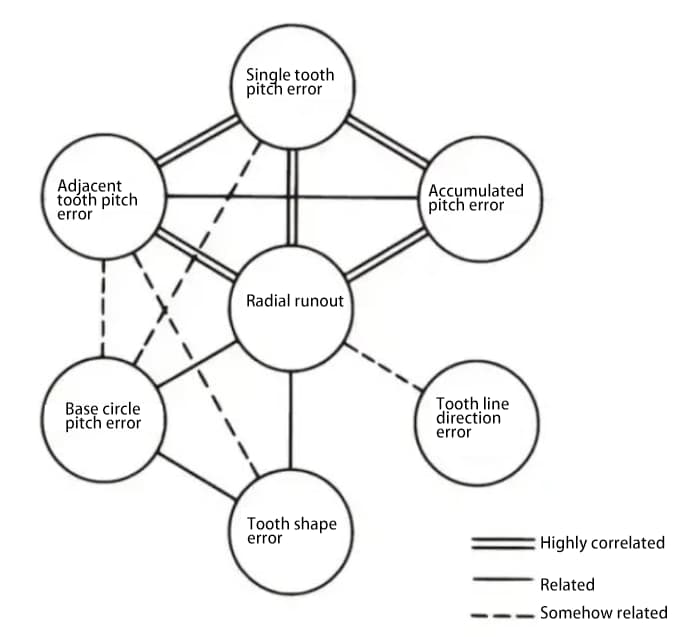
Различные составляющие точности зубчатых колес связаны друг с другом. Как правило, радиальное биение сильно коррелирует с другими погрешностями, а также существует сильная корреляция между различными погрешностями шага.
Угол спирали на нормальном цилиндрическом участке:
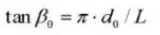
Угол спирали на базовом цилиндре:
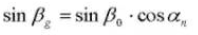
Толщина зуба Угол центрирования:
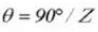
Диаметр штыря:
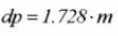
Коэффициент коррекции межцентрового расстояния:
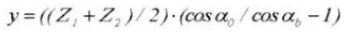
Расчет стандартных цилиндрических зубчатых колес (шестерня ①, зубчатое колесо ②)
1. Количество зубьев на шестерне Стандарт
2. Стандартный профиль шестерни с прямыми зубьями
3. Модуль m
4. Угол давления
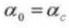
5. Количество зубов
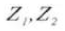
6. Эффективная глубина зуба
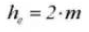
7. Вся глубина зуба
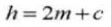
8. Зазор между зубьями
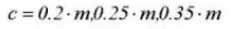
9. Контрольный диаметр делительной окружности
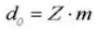
10. Наружный диаметр
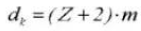
11. Диаметр корня
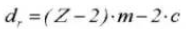
12. Диаметр базовой окружности
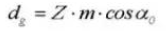
13. Круговой шаг
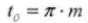
14. Нормальный диаметральный шаг
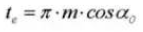
15. Толщина кругового зуба
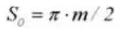
16. Толщина хордального зуба
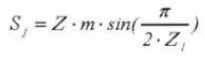
17. Высота зуба щупа редуктора
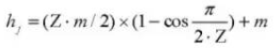
18. Количество зубов по всей длине
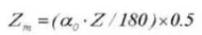
19. Толщина зуба в поперечном направлении
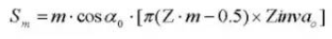
20. Диаметр штыря
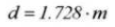
21. Цилиндрический измерительный размер
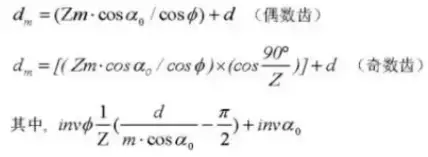
Формула для расчета смещенных цилиндрических зубчатых колес (шестерня ①, передача ②):
1. Поперечный профиль зубьев шестерни
2. Коэффициент контакта профиля зубьев инструмента
3. Модуль m
4. Угол давления
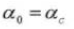
5. Количество зубьев Z
6. Эффективная глубина зуба
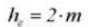
7. Вся глубина зуба
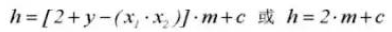
8. Люфт шестерни C
9. Коэффициент поперечного контакта X
10. Центральное расстояние
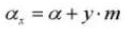
11. Контрольный диаметр делительной окружности
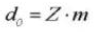
12. Угол рабочего давления
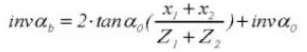
13. Диаметр делительной окружности
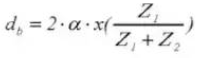
14. Наружный диаметр
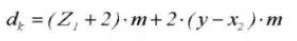
15. Диаметр дополнения
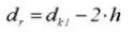
16. Диаметр шага
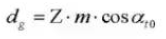
17. Круговой шаг
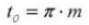
18. Нормальный диаметральный шаг
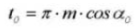
19. Толщина кругового зуба
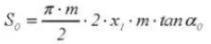
20. Толщина хордального зуба
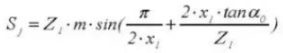
21. Высота зубьев зубчатого верньерного калипера
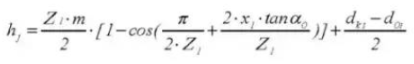
22. Количество зубов по всей длине
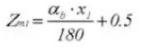
23. Толщина зуба в поперечном направлении
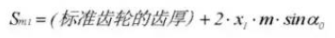
24. Диаметр наконечника
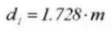
25. Поперечный измерительный размер
Формула для расчета стандартных косозубых передач (нормальная система) (шестерня ①, передача ②)
1. Стандартный профиль зубьев шестерни
2. Справочная секция системы нормального профиля зуба
3. Инструментальный профиль зубьев косозубой шестерни
4. Модуль
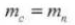
5. Угол давления
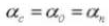
6. Количество зубов
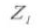
7. Направление спирали
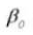
8. Эффективная глубина зуба
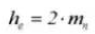
9. Вся глубина зуба
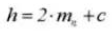
10. Угол переднего давления
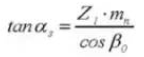
11. Центральное расстояние
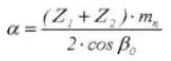
12. Контрольный диаметр делительной окружности
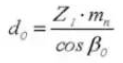
13. Наружный диаметр
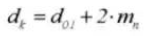
14. Диаметр корня
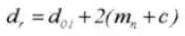
15. Диаметр шага
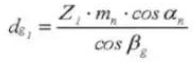
16. Угол спирали на базовом круге
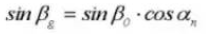
17. Питч
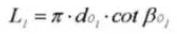
18. Круговой шаг (нормальная система)
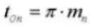
19. Нормальный диаметральный шаг (нормальная система)
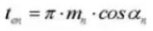
20. Толщина кругового зуба (нормальная система)
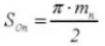
21. Эквивалентное число зубьев стандартной цилиндрической передачи
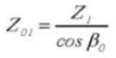
22. Толщина хордального зуба
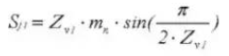
23. Зубчатый штангенциркуль Глубина зубьев
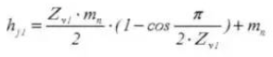
24. Количество зубов по всей длине
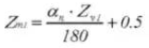
25. Толщина зуба в поперечном направлении
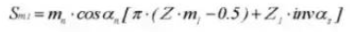
26. Диаметр наконечника
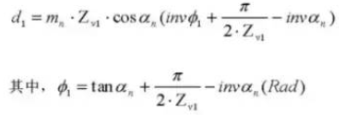
27. Цилиндрический измерительный размер
28. Люфт шестерни f
Формула для расчета смещенных косозубых передач (нормальная система) (шестерня ①, зубчатое колесо ②):
1. Смещение профиля зубьев шестерни
2. Справочная секция системы нормального профиля зуба
3. Инструментальный профиль зубьев косозубой шестерни
4. Модуль (нормальная система)
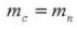
5. Угол давления (нормальная система)
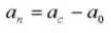
6. Количество зубов
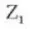
7. Направление спирали
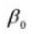
8. Эффективная глубина зуба
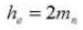
9. Вся глубина зуба
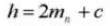
10. Коэффициент поперечного контакта
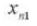
11. Центральное расстояние
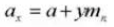
12. Обычный модуль
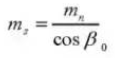
13. Угол переднего давления (нормальная система)
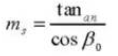
14. Эквивалентное число зубьев стандартной цилиндрической передачи
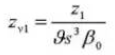
15. Нормальный угол давления в системе
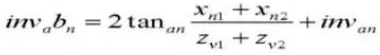
16. Контрольный диаметр делительной окружности
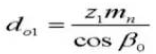
17. Наружный диаметр
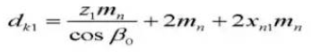
18. Диаметр шага соприкасающихся зубьев
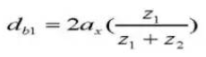
19. Диаметр шага
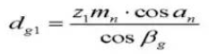
20. Угол спирали на базовом цилиндре
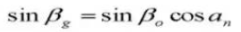
21. Толщина кругового зуба
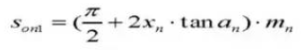
22. Толщина хордального зуба
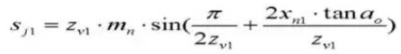
23. Высота зубьев верньерного штангенциркуля.
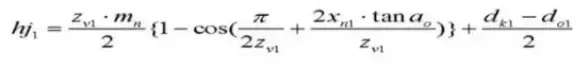
24. Количество зубов по всей длине
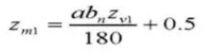
25. Толщина зуба в поперечном направлении
26. Диаметр штыря.
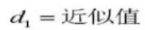
27. Цилиндрический измерительный размер
Как основатель MachineMFG, я посвятил более десяти лет своей карьеры металлообрабатывающей промышленности. Мой обширный опыт позволил мне стать экспертом в области производства листового металла, механической обработки, машиностроения и станков для обработки металлов. Я постоянно думаю, читаю и пишу об этих предметах, постоянно стремясь оставаться на переднем крае своей области. Позвольте моим знаниям и опыту стать преимуществом для вашего бизнеса.
RU 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
KO