¿Le cuesta diseñar piezas de chapa metálica precisas? Descubra los secretos del factor K, un concepto crucial en la fabricación de chapa metálica. En este artículo, nuestro ingeniero mecánico experto desmitifica el factor K, explicando su relación con la capa neutra y proporcionando métodos prácticos de cálculo. Descubra cómo el dominio del factor K puede revolucionar sus diseños de chapa metálica y garantizar el éxito de la fabricación.
Este artículo analiza en profundidad el factor K, un concepto crucial en el diseño y la fabricación de chapas metálicas. Abarca la definición del factor K, su relación con la capa neutra y los métodos de cálculo y calibración del factor K.
El artículo también analiza los factores que influyen en el factor K, como las propiedades del material y los parámetros de flexión, y ofrece orientaciones prácticas para determinar el valor óptimo del factor K para diversas aplicaciones.
El factor K es un concepto fundamental que debe comprender cualquiera que desee dominar el diseño de chapa metálica en SolidWorks y la fabricación de chapa metálica en general. En pocas palabras, el factor K es la relación entre la distancia entre la capa neutra y la superficie interior de la curva (t) y el grosor de la chapa metálica (T). Matemáticamente, se expresa como
K = t / T
Como se desprende de la definición, el factor K es siempre un valor constante entre 0 y 1. Comprender el factor K y sus implicaciones es fundamental para crear diseños precisos de piezas de chapa metálica que puedan fabricarse con éxito.
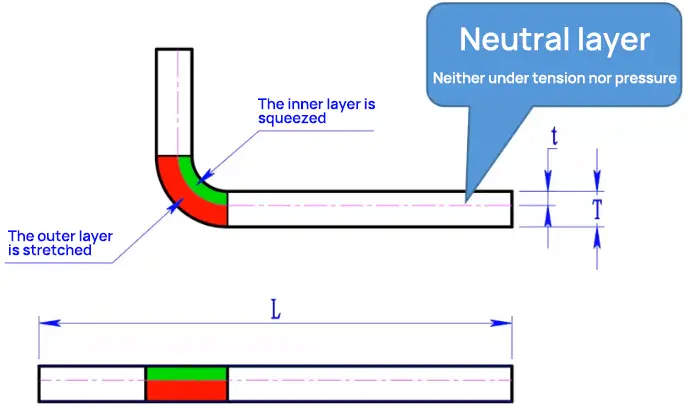
Para comprender plenamente el factor K, es esencial entender el concepto de capa neutra. Cuando se dobla una pieza de chapa metálica, el material cercano a la superficie interior de la curva experimenta compresión, y la intensidad aumenta más cerca de la superficie. A la inversa, el material cercano a la superficie exterior experimenta un estiramiento, cuya intensidad aumenta más cerca de la superficie.
Suponiendo que la chapa esté compuesta por capas finas apiladas (como ocurre con la mayoría de los metales), debe existir una capa en el medio que no experimente ni compresión ni estiramiento durante la flexión. Esta capa se denomina capa neutra. La capa neutra es fundamental para determinar el factor K y, en consecuencia, la tolerancia a la flexión y las dimensiones planas de una pieza de chapa metálica.
Aunque la capa neutra no es visible ni tangible, ya que se encuentra dentro de la chapa metálica, su posición viene determinada por las propiedades inherentes del material. Por consiguiente, el factor K también depende de las propiedades del material.
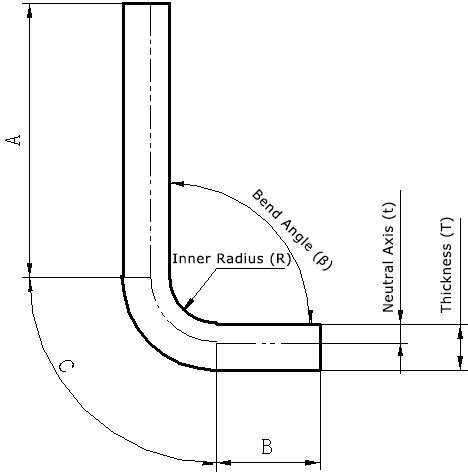
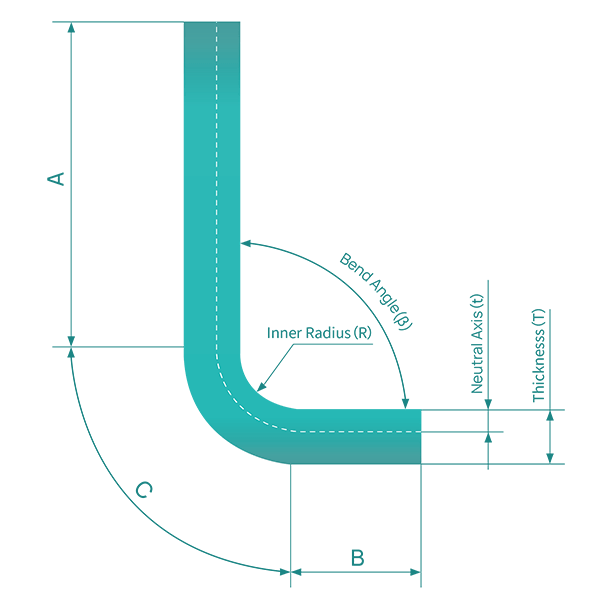
Una idea clave del concepto de capa neutra es que la longitud desplegada (patrón plano) de una pieza de chapa metálica doblada es igual a la longitud de la capa neutra. En referencia al diagrama anterior, esto puede expresarse como:
Longitud sin plegar = longitud recta A + longitud recta B + longitud de arco C (longitud de la capa neutra en la zona de plegado)
Comprender esta relación es crucial para calcular con precisión las dimensiones de los patrones planos basándose en el factor K y el margen de curvatura, que están influidos por las propiedades del material.
El factor K es un valor independiente que caracteriza el comportamiento de flexión y despliegue de la chapa metálica en una amplia gama de parámetros geométricos. También se utiliza de forma independiente para calcular la tolerancia a la flexión (BA) en diversas condiciones, como:
Saber calcular el factor K es esencial para diseñar y fabricar chapas metálicas con precisión.
Las siguientes ilustraciones ofrecen una explicación visual detallada del concepto de factor K:
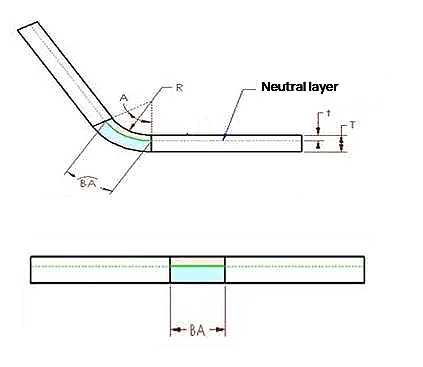
En la sección transversal de una pieza de chapa metálica existe una capa neutra o eje. El material de esta capa neutra dentro de la región de flexión no experimenta ni compresión ni estiramiento, por lo que es la única zona que permanece indeformada durante la flexión. En el diagrama, la capa neutra está representada por la intersección de las regiones rosa (compresión) y azul (estiramiento).
Una idea clave es que si la capa neutra permanece indeformada, la longitud del arco de la capa neutra dentro de la región de flexión debe ser igual tanto en el estado doblado como en el aplanado de la pieza de chapa metálica. Este principio constituye la base para el cálculo de los márgenes de curvatura y las dimensiones del patrón plano mediante el factor K.
Por lo tanto, la sobremedida de flexión (BA) debe ser igual a la longitud del arco de la capa neutra en la zona de flexión de la pieza de chapa. Este arco se representa en verde en la figura.
La posición de la capa neutra en la chapa metálica depende de determinadas propiedades del materialcomo la ductilidad.
Suponiendo que la distancia entre la capa de chapa neutra y la superficie es "t", es decir, la profundidad desde la superficie de la pieza de chapa hasta la chapa material metálico en la dirección del espesor es t.
Por lo tanto, el radio del arco de la capa de chapa neutra puede expresarse como (R+t).
Utilizando esta expresión y la ángulo de flexión, la longitud del arco de la capa neutra (BA) puede expresarse como:
Para simplificar la definición de la capa neutra en chapa metálica y considerando la aplicabilidad a todos los espesores de material, se introduce el concepto de factor k. Concretamente, el factor k es la relación entre el espesor de la posición de la capa neutra y el espesor total de la pieza de chapa metálica, es decir:
Por lo tanto, el valor de K está siempre comprendido entre 0 y 1. Si el factor k es 0,25, significa que la capa neutra está situada a 25% del espesor del material de chapa, y si es 0,5, significa que la capa neutra está situada a la mitad de todo el espesor, y así sucesivamente.
Combinando las dos ecuaciones anteriores, podemos obtener la siguiente ecuación:
Algunos valores, como A, R y T, vienen determinados por la forma geométrica real.
Para ayudarle a determinar el valor del factor K, ponemos a su disposición dos calculadoras que se adaptan a distintos escenarios de entrada de datos. Aunque los resultados finales pueden diferir ligeramente, ambas calculadoras satisfarán sus necesidades.
Si conoce la tolerancia de la curva y el radio interior de la curva, utilice esta calculadora para determinar el factor K y la distancia de la superficie interior al eje neutro (t).
Entradas:
Salidas:
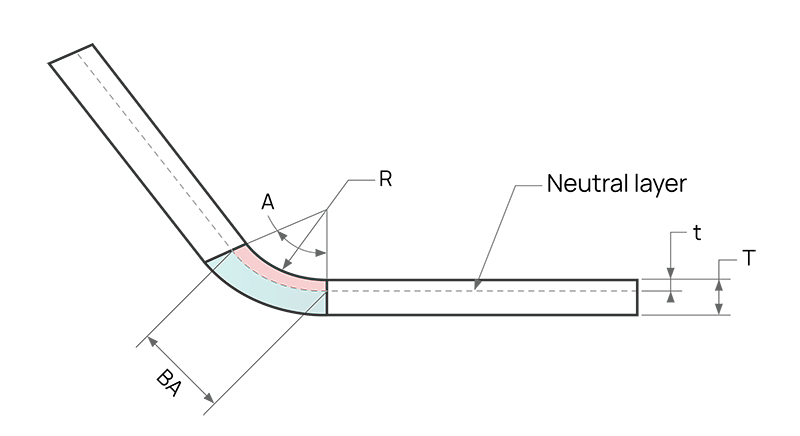
Si sólo conoce el radio de curvatura interior y el grosor del material, utilice esta calculadora para determinar el factor K.
Entradas:
Salidas:
Estas calculadoras proporcionan una forma cómoda de determinar rápidamente el factor K y la posición del eje neutro para sus proyectos de diseño de chapa metálica.
A partir de los cálculos anteriores, podemos deducir la fórmula para calcular el factor K:
Dónde:
Cálculo de muestras:
Veamos un ejemplo de cálculo a partir de la siguiente información:
La fórmula para calcular el factor K es
Paso 1: Sustituye los valores dados en la fórmula del factor K:
K = (2.1 × 180/(3.14 × 90) - 1)/1
Paso 2: Simplifica la ecuación:
K ≈ 0.337
Por lo tanto, para los parámetros dados, el factor K es aproximadamente 0,337.
Este ejemplo muestra cómo aplicar la fórmula de cálculo del factor K para determinar el factor K para un escenario específico de plegado de chapa metálica.
A continuación se indican los factores K de los materiales metálicos más comunes.
Cuadro del factor K
| Espesor (SPCC/SECC) | Factor K (Todos los ángulos, incluido el ángulo R) |
| 0.8 | 0.615 |
| 1 | 0.45 |
| 1.2 | 0.35 |
| 1.5 | 0.348 |
| 2 | 0.455 |
| 3 | 0.349 |
| 4 | 0.296 |
Cuadro de deducción por flexión
| Espesor (SPCC/SECC) | Deducción por flexión (sólo aplicable a esquinas de 90º) |
| 0.8 | 1 |
| 1 | 1.5 |
| 1.2 | 2 |
| 1.5 | 2.5 |
| 2 | 3 |
| 3 | 5 |
| 4 | 7 |
| 5 | 10 |
La siguiente tabla muestra los valores de tolerancia a la flexión obtenidos por un fabricante específico para diversos materiales y espesores. Tenga en cuenta que estos valores son sólo de referencia y pueden no ser de aplicación universal.
| Grosor del material (T) | SPCC | Al | SUS | Cobre |
| 0.8 | 1.4 | 1.4 | 1.5 | – |
| 1.0 | 1.7 | 1.65 | 1.8 | – |
| 1.2 | 1.9 | 1.8 | 2.0 | – |
| 1.5 | 2.5 | 2.4 | 2.6 | – |
| 2.0 | 3.5 | 3.2 | 3.6 | 37 (R3) |
| 2.5 | 4.3 | 3.9 | 4.4 | – |
| 3.0 | 5.1 | 4.7 | 5.4 | 5.0 (R3) |
| 3.5 | 6.0 | 5.4 | 6.0 | |
| 4.0 | 7.0 | 6.2 | 7.2 | 6.9 (R3) |
Nota: Para el cobre, los valores de tolerancia de curvatura son coeficientes cuando el radio de curvatura interior es R3. Si se utiliza un punzón agudo para el doblado, consulte la tolerancia de doblado para la aleación de aluminio o determine el valor mediante un doblado de prueba.
Para entender por qué el factor K no puede ser superior a 0,5, es esencial comprender los conceptos de factor K y capa neutra.
Curvar una pieza de chapa implica crear un pequeño arco, similar al curvado con rodillo pero con un radio menor. Independientemente del método utilizado, es imposible conseguir un ángulo recto perfecto, y siempre habrá un ligero arco. El radio de la pieza está directamente relacionado con el radio inferior de la matriz: un radio menor de la matriz se traduce en un radio menor de la pieza, y viceversa.
Las piezas de chapa metálica tienen un grosor y, cuando se doblan en forma de arco, las dimensiones de la superficie interior se reducen mientras que las de la superficie exterior aumentan. Este fenómeno da lugar a la sobremedida de doblado. Por ejemplo, al doblar una pieza en forma de ángulo con un diámetro exterior de 20 x 20, siempre se desplegará a menos de 40, independientemente del grosor de la chapa. Esto se debe a que las dimensiones de la superficie exterior aumentan tras el doblado. Si el tamaño desplegado está diseñado para ser 40, el tamaño doblado será 20 en un lado y más de 20 en el otro.Tradicionalmente, se creía que, independientemente del grosor de la chapa y de la cantidad de cambio dimensional en las superficies interior y exterior, el tamaño de la capa intermedia permanecería constante. Esta capa intermedia se conoce como capa neutra.
Con la creciente demanda de precisión dimensional de los productos, se ha observado que la cantidad de reducción en el interior no siempre coincide con la cantidad de expansión en el exterior. Especialmente en el caso de pequeños arcos resultantes (como curvas), el interior tiende a reducirse 0,3, mientras que el exterior aumenta 1,7. Esto revela que la capa neutra, cuyo tamaño permanece constante, no se encuentra necesariamente en el centro del espesor de la chapa, sino más cerca del interior. El factor K se define como la distancia del interior a la capa neutra dividida por el espesor total de la chapa.
La capa neutra puede estar, como máximo, en la mitad del espesor de la chapa. Por lo tanto, la distancia desde el interior hasta el centro dividida por todo el espesor de la chapa es 0,5, lo que da como resultado un valor máximo del factor K de 0,5. Estos factores explican por qué el factor K en chapa metálica no debe superar 0,5.
Incluso para el mismo material, el factor K en la transformación real no es constante y se ve afectado por la tecnología de transformación. En la fase de deformación elástica del plegado de chapas metálicas, el eje neutro se sitúa en el centro del espesor de la chapa. Sin embargo, a medida que aumenta la deformación por flexión de la pieza, el material sufre principalmente deformación plástica, que es irrecuperable.
En este punto, la capa neutra se desplaza hacia el interior de la curva a medida que cambia el estado de deformación. Cuanto más grave sea la deformación plástica, mayor será el desplazamiento hacia el interior de la capa neutra.
Para reflejar la intensidad de la deformación plástica durante la flexión de la placa, podemos utilizar el parámetro R/T, donde R representa el radio de curvatura interior y T representa el espesor de la placa. Una relación R/T menor indica un mayor nivel de deformación de la placa y un mayor desplazamiento hacia el interior de la capa neutra.
La tabla siguiente muestra los datos correspondientes a chapas de sección rectangular en determinadas condiciones de transformación. A medida que aumenta R/T, aumenta también el factor K de posición de la capa neutra.
| R/T | K |
| 0.1 | 0.21 |
| 0.2 | 0.22 |
| 0.3 | 0.23 |
| 0.4 | 0.24 |
| 0.5 | 0.25 |
| 0.6 | 0.26 |
| 0.7 | 0.27 |
| 0.8 | 0.3 |
| 1 | 0.31 |
| 1.2 | 0.33 |
| 1.5 | 0.36 |
| 2 | 0.37 |
| 2.5 | 0.4 |
| 3 | 0.42 |
| 5 | 0.46 |
| 75 | 0.5 |
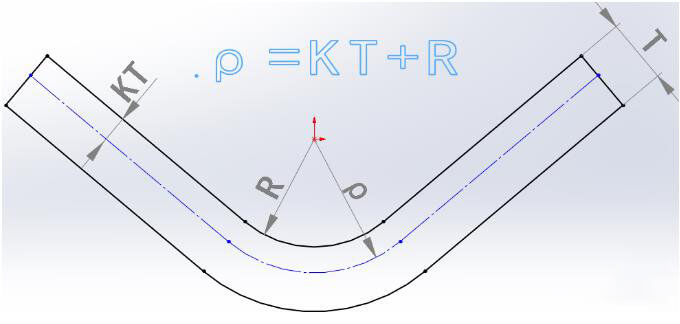
El radio de la capa neutra (ρ) puede calcularse mediante la siguiente fórmula:
ρ = R + KT
Dónde:
Una vez determinado el radio de la capa neutra, se puede calcular su longitud desarrollada basándose en la geometría y, posteriormente, derivar la longitud desarrollada de la lámina.
Generalmente, bajo las mismas condiciones de doblado, los materiales de chapa más blandos tienen valores K más bajos y mayores desplazamientos hacia el interior de la capa neutra.El Machinery's Handbook proporciona tres tablas de doblado estándar aplicables al doblado a 90 grados, como se muestra a continuación:
| Cuadro | Material | Factor K |
| # 1 | Latón blando, cobre | 0.35 |
| # 2 | Latón duro, cobre, acero dulce, aluminio | 0.41 |
| # 3 | Latón duro, bronce, frío acero laminadoacero para muelles | 0.45 |
Estas tablas demuestran cómo influyen las propiedades de los materiales en el factor K y en la posición de la capa neutra.
En el caso de las curvas con radios interiores más pequeños, el ángulo de curvatura también puede afectar al cambio del factor K. A medida que aumenta el ángulo de curvatura, la capa neutra experimenta un mayor desplazamiento hacia el lado interior de la curva. Esta relación entre el ángulo de curvatura y el desplazamiento de la capa neutra es especialmente significativa en las curvas de radio reducido y debe tenerse en cuenta a la hora de determinar el factor K adecuado para una determinada pieza de chapa metálica.
En los cálculos de plegado de chapa metálica, a menudo es necesario calibrar el factor K. Pero, ¿por qué es necesaria esta calibración?
En SolidWorks, el valor de deducción de curvatura para curvas de menos de 90 grados sólo se calcula mediante introducción manual, lo que puede resultar engorroso. Para evitar este cálculo manual, se utiliza en su lugar el factor K. Sin embargo, determinar con precisión el factor K para diferentes espesores de chapa metálica requiere calibración.
Aquí tienes un análisis paso a paso del proceso de calibración del factor K:
Repita este proceso de calibración para diferentes espesores de chapa y registre los valores calibrados del factor K en una tabla para futuras consultas.
Para determinar el valor óptimo del factor K para el plegado de chapa metálica en función de las diferentes propiedades del material, es esencial comprender el papel y la importancia del factor K. El factor K es un valor independiente que describe cómo se dobla y despliega la chapa metálica en función de diversos parámetros geométricos. También se utiliza para calcular la compensación de curvatura para diferentes espesores de material, radios de curvatura y ángulos de curvatura. La elección del factor K adecuado es crucial para garantizar el despliegue y plegado precisos de las piezas de chapa metálica.
El proceso de determinación del valor óptimo del factor K basado en las propiedades del material puede resumirse en los siguientes pasos:
Siguiendo estos pasos y teniendo en cuenta las propiedades del material, los valores por defecto, los ajustes experimentales, las tablas de deducción de plegado y los parámetros de plegado adicionales, podrá determinar el valor óptimo del factor K para su aplicación específica de plegado de chapa metálica.
P: ¿Cuál es la gama típica de valores del factor K para los materiales comunes?
R: El factor K suele oscilar entre 0,3 y 0,5, dependiendo del material. Por ejemplo, el latón blando y el cobre tienen un factor K en torno a 0,35, mientras que el latón duro, el bronce y el acero laminado en frío tienen un factor K cercano a 0,45.
P: ¿Cómo elijo el factor K adecuado para mi diseño de chapa metálica?
R: Para seleccionar el factor K adecuado, tenga en cuenta las propiedades del material, el espesor, el radio de curvatura y el ángulo de curvatura. Consulte las tablas estándar de factores K o utilice las calculadoras suministradas para determinar el valor óptimo para su aplicación específica.
En conclusión, el factor K es un concepto fundamental en el diseño y la fabricación de chapas metálicas. Al comprender su relación con la capa neutra, las propiedades del material y los parámetros de plegado, los diseñadores e ingenieros pueden crear patrones planos precisos y conseguir márgenes de plegado exactos. Dominar el factor K es esencial para producir piezas y conjuntos de chapa metálica de alta calidad.
Otras lecturas y recursos
Para profundizar en el curvado de chapa y otros conceptos relacionados, explore los siguientes recursos:
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
DE 
FR 
IT 
NL 
PT 
RU 