¿Alguna vez ha tenido problemas para desplegar con precisión piezas de chapa metálica? Este artículo explora el arte y la ciencia que hay detrás de los cálculos de desdoblamiento de chapa metálica. Descubra los conceptos clave, las fórmulas y las técnicas utilizadas por ingenieros experimentados para desplegar con precisión geometrías complejas. Aprenda a aplicar estos principios a sus propios diseños y agilice su proceso de fabricación.
El primer paso en el proceso de fabricación de chapas metálicas es el desdoblamiento de las geometrías y el cuerpo coherente. La precisión y corrección del desdoblamiento de la muestra repercute directamente en la calidad de la pieza final.
En el pasado, debido a las limitaciones de las herramientas de cálculo, se utilizaba el método de proyección para ampliar la muestra en un plano con una relación 1:1 y medir la longitud real de la línea del plano requerida.
Sin embargo, este método es complicado e ineficaz, y no puede satisfacer las demandas actuales de producción.
Con los avances en herramientas de cálculo, como las calculadoras electrónicas y el uso generalizado de ordenadores, chapa metálica El desdoblamiento puede realizarse ahora mediante métodos de cálculo.
Para estandarizar el método de cálculo del coeficiente de desdoblamiento de la chapa por parte de los técnicos, minimizar las desviaciones dimensionales de los productos tras el plegado y facilitar la autoinspección por parte del personal del taller y la reinspección por parte de los inspectores de calidad, existe una norma y una base unificadas para el coeficiente de desdoblamiento.
Como resultado, la norma de cálculo del coeficiente de despliegue de la chapa se ha estandarizado cada vez más.
Método de despliegue de la capa neutra
En el proceso de flexión, la capa exterior sufre esfuerzos de tracción, mientras que la interior experimenta esfuerzos de compresión. La capa de transición entre el esfuerzo de tracción y el de compresión se denomina capa neutra. La longitud de la capa neutra durante el plegado sigue siendo la misma que antes del plegado, lo que la convierte en la referencia para determinar la longitud desplegada de la pieza plegada.
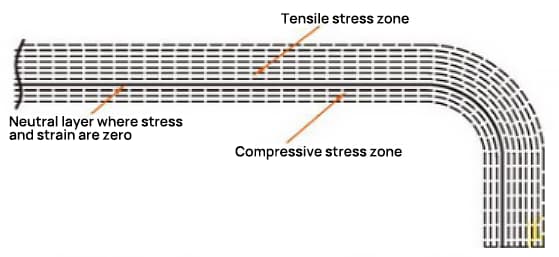
La ubicación de la capa neutra depende del grado de deformación.
La posición de la capa neutra no sólo está relacionada con el radio de curvatura, el grosor de la chapa, el coeficiente de desplazamiento hacia el interior, etc., sino también con factores como el método de procesamiento, la forma de la chapa y el tamaño.
Por lo tanto, la posición de la capa neutra sólo puede determinarse de forma aproximada, y en las aplicaciones prácticas se suelen utilizar valores aproximados para el cálculo.
La fórmula de cálculo para la dimensión de longitud L de la capa neutra es:
Entre ellas,
Mediante el uso de software 3D para realizar simulaciones y cálculos de diversos espesores, ángulos y radios, junto con las prácticas de fabricación in situ, hemos recopilado un conjunto de valores de factor K. Los valores específicos figuran en la tabla 1.
Tabla 1: Valores K del coeficiente de la capa neutra
| r/t | ≤05 | 0.6 | 0.8 | 1 | 1.2 | 1.3 | 1.5 | 2 | 2.5 | 3.0 | 4.0 | 5.0 | 6.0 | ≥8 |
| k | 026 | 0.28 | 0.30 | 0.32 | 0.33 | 0.34 | 0.36 | 0.38 | 0.39 | 0.4 | 0.42 | 0.44 | 0.46 | 0.5 |
Cálculo de despliegue rápido para curvas de 90
En la figura 9 se muestra el diagrama de desdoblamiento de una curva de 90°. En los últimos años, hemos utilizado software 3D como CATIA y SOLIDWORKS para el modelado de chapa metálica con el fin de calcular las dimensiones de desdoblamiento.
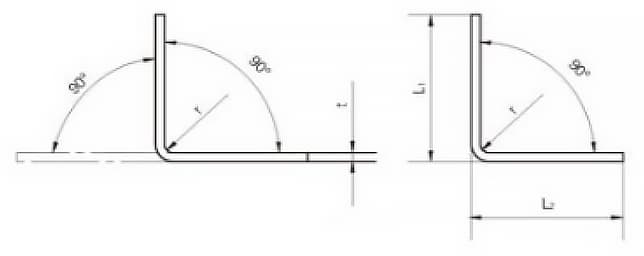
Mediante repetidas comprobaciones, se ha observado que cuando el ángulo de flexión en frío de los productos planos de acero es de 90°, la fórmula para calcular la longitud desplegada L es:
L = L1 + L2 - A
Dónde,
Tabla 2 Tabla de parámetros de flexión a 90
| Espesor t/mm | Radio de inclinación r/mm | |||||||||||
| 1 | 1.2 | 16 | 2 | 25 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | |
| Valor de compensación A mm | ||||||||||||
| 1 | -1.92 | -1.97 | -2.10 | -2.23 | -2.41 | -2.59 | -2.97 | -3.36 | -3.79 | -4.65 | -5.51 | -6.37 |
| 1.5 | -2.90 | -3.02 | -3.18 | -3.34 | -3.70 | -4.07 | -4.45 | -5.26 | -6.11 | -6.97 | ||
| 2 | -3.84 | -3.98 | -4.13 | -4.46 | -4.81 | -5.18 | -5.94 | -6.72 | -7.58 | |||
| 2.5 | -4.80 | -4.93 | -5.24 | -5.57 | -5.93 | -6.66 | -7.42 | -8.21 | ||||
| 3 | -5.76 | 6.04 | -6.35 | -6.69 | -7.40 | -8.14 | -8.91 | |||||
| 4 | -7.7 | -7.95 | -8.26 | -8.92 | -9.62 | -10.36 | ||||||
| 5 | -9.6 | -9.87 | -10.48 | -11.15 | -11.85 | |||||||
| 6 | -11.5 | -12.08 | -12.71 | -13.38 | ||||||||
| 8 | -15.4 | -15.9 | -16.51 | |||||||||
| 10 | -19.2 | -19.73 | ||||||||||
| 12 | 23.01 | |||||||||||
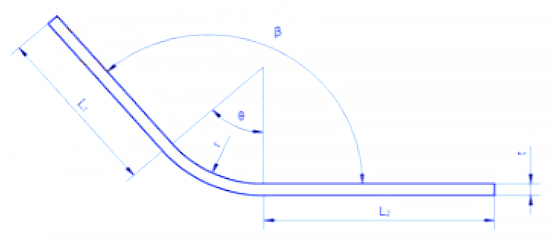
Cuando el radio de curvatura es grande y el ángulo de flexión es pequeño, el grado de deformación es bajo y la capa neutra está cerca del centro del espesor de la chapa.
Sin embargo, cuando el radio de curvatura (R) se hace más pequeño y el ángulo de flexión (θ) aumenta, el grado de deformación también aumenta y la capa neutra se desplaza hacia el lado interior del centro de flexión. La distancia de la capa neutra al lado interior de la chapa se denota por λ, y el espesor del material se denota por T.
La fórmula básica para calcular la longitud de desdoblamiento:
Longitud de despliegue = tamaño interior del material + tamaño interior del material + cantidad de compensación.
También puede utilizar la siguiente calculadora para calcular la longitud de desdoblamiento de la chapa:

A continuación se describen uno a uno los algoritmos de desdoblamiento de varias características de curvatura.
R = 0mm, θ = 90° (Nota: Cuando R ≤ 1,0mm, se trata como R = 0mm).
L = A + B + K
En la producción real, la matriz superior de doblado puede llevar un ángulo R, o puede haber un ángulo R inferior a 1 mm, o la elección del troquel inferiorpuede ser grande, entre otras razones, lo que da lugar a un coeficiente de flexión pequeño. En consecuencia, el coeficiente de flexión de cada espesor de placa de material se presenta en la Tabla 1 basado en valores empíricos reales.
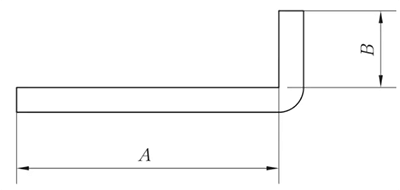
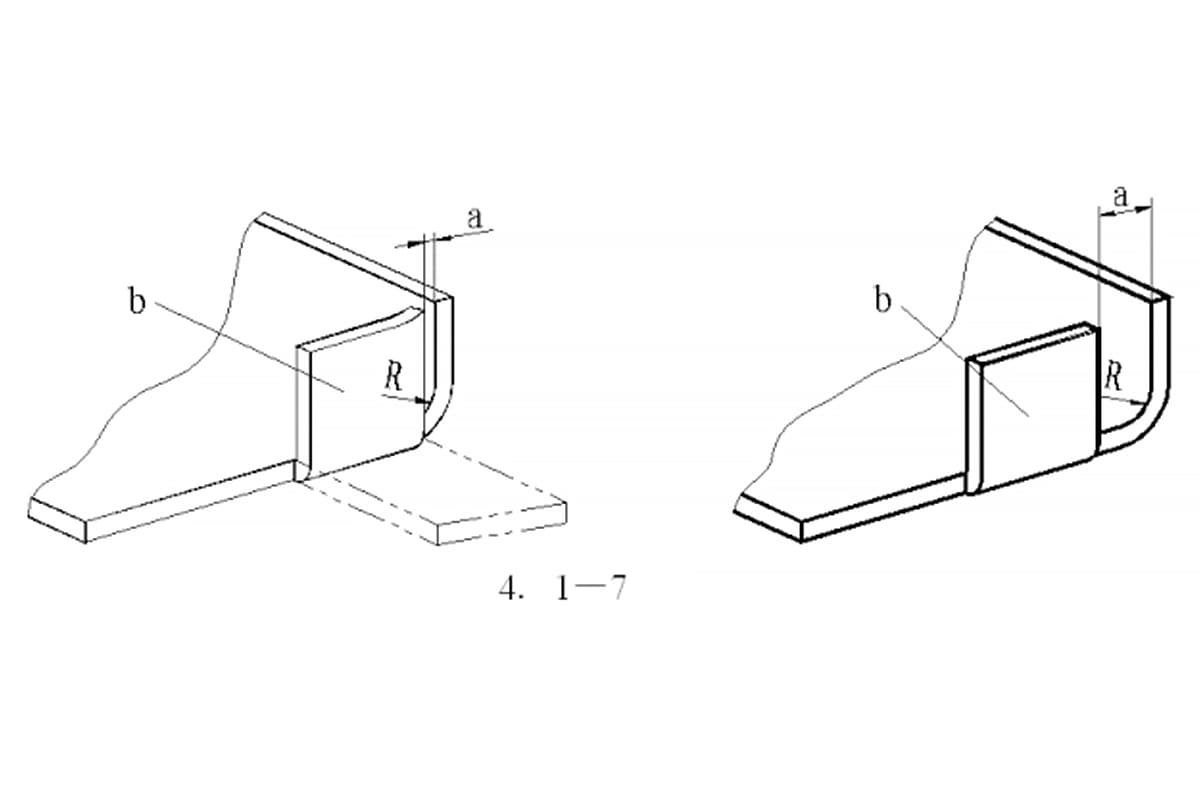
Fig. 1 Diagrama esquemático de la flexión general I
R ≠ 0mm y θ = 90°.
L = A + B + K (K es la longitud de arco de la capa neutra )
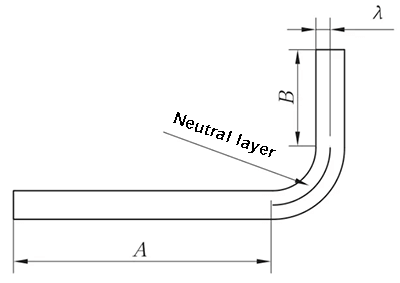
Fig. 2 Diagrama esquemático de la flexión general II
R = 0mm, θ ≠ 90°
L = A + B + K'
Nota: K es la cantidad de compensación a 90°.
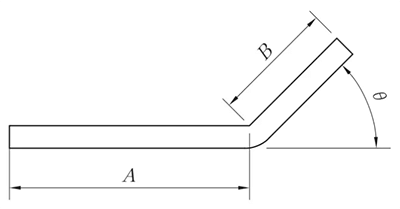
R ≠ 0mm, θ ≠ 90°
L = A + B + K
(K toma la longitud de arco de la capa neutra)
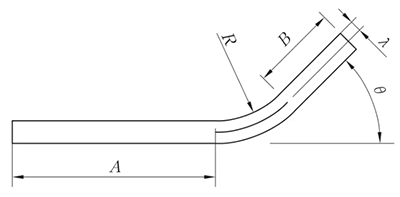
Fig. 4 Flexión general IV diagrama de flexión
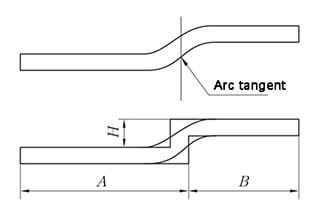
El método de desplegado es equivalente al método de plegado en Z de bordes rectos paralelos, y la medición de la altura se muestra en la figura 6.
El ángulo θ se considera un desdoblamiento de 90°.
Para 0 < T ≤ 1,6mm, λ es igual a 0,5T.
Cuando T es superior a 1,6 mm, λ es igual a 0,4T.
Z-Fold, también denominado Plegado offsetEn función del ángulo de conformación, se distingue entre plegado en ángulo recto y plegado en ángulo biselado, y el método de procesamiento viene determinado por la altura de desplazamiento.
Cuando la altura de desplazamiento, h, es inferior a 3,5 veces el grosor del material, troqueles offset o se utilizan matrices intercambiables para el conformado.
Si la altura de desplazamiento es superior a 3,5 veces el grosor del material, se emplea el conformado positivo y negativo normal.
Cuando la longitud del borde biselado es inferior a 3,5 veces el grosor del material, se utilizan troqueles de desplazamiento o troqueles cambiables para el conformado.
Si la longitud del borde biselado es superior a 3,5 veces el grosor del material, se aplica el plegado normal de uno positivo y uno negativo.
(1) Cuando H < 3,5T, sólo entonces se puede procesar mediante plegado offset.
L = A + B + H
(si H ≤ T, entonces compensar 0,2mm)
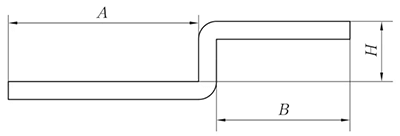
Fig. 5 Esquema del desplazamiento de la regla
(2) Desplazamiento no paralelo de la regla
El método de expansión es el mismo que el método de plegado en Z con borde recto paralelo, y el valor de la altura se muestra en la figura 6.
El ángulo θ puede considerarse desdoblado a 90°.
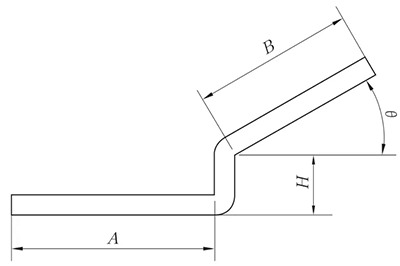
Fig. 6 Esquema del desplazamiento de la regla no paralela
(3) Desplazamiento del borde recto - el segmento de transición es tangente a dos arcos
Cuando el desplazamiento del borde recto se despliega en el punto tangente de dos arcos circulares, se crea una línea vertical en el punto tangente de los dos arcos circulares en la superficie exterior del sustrato. A continuación, el material se desplaza un grosor hacia el interior, como se muestra en la figura 7, para su procesamiento y se despliega utilizando el método Z-Fold 1 (Straight-Edge Offset).
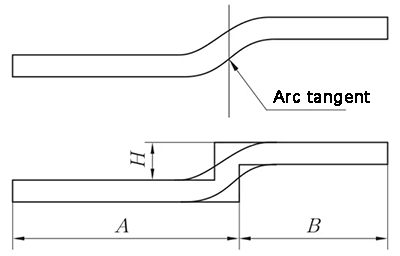
Fig. 7 Diagrama de desplazamiento de aristas rectas - segmento de transición es tangente a dos arcos de círculo
Cuando H < 2T, el algoritmo de desdoblamiento es el siguiente de acuerdo con el procesamiento offset.
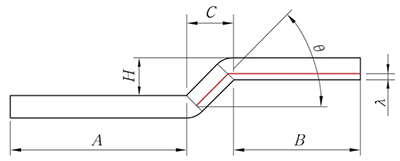
Fig. 8 Diagrama del desplazamiento del borde biselado
L = A + B - K
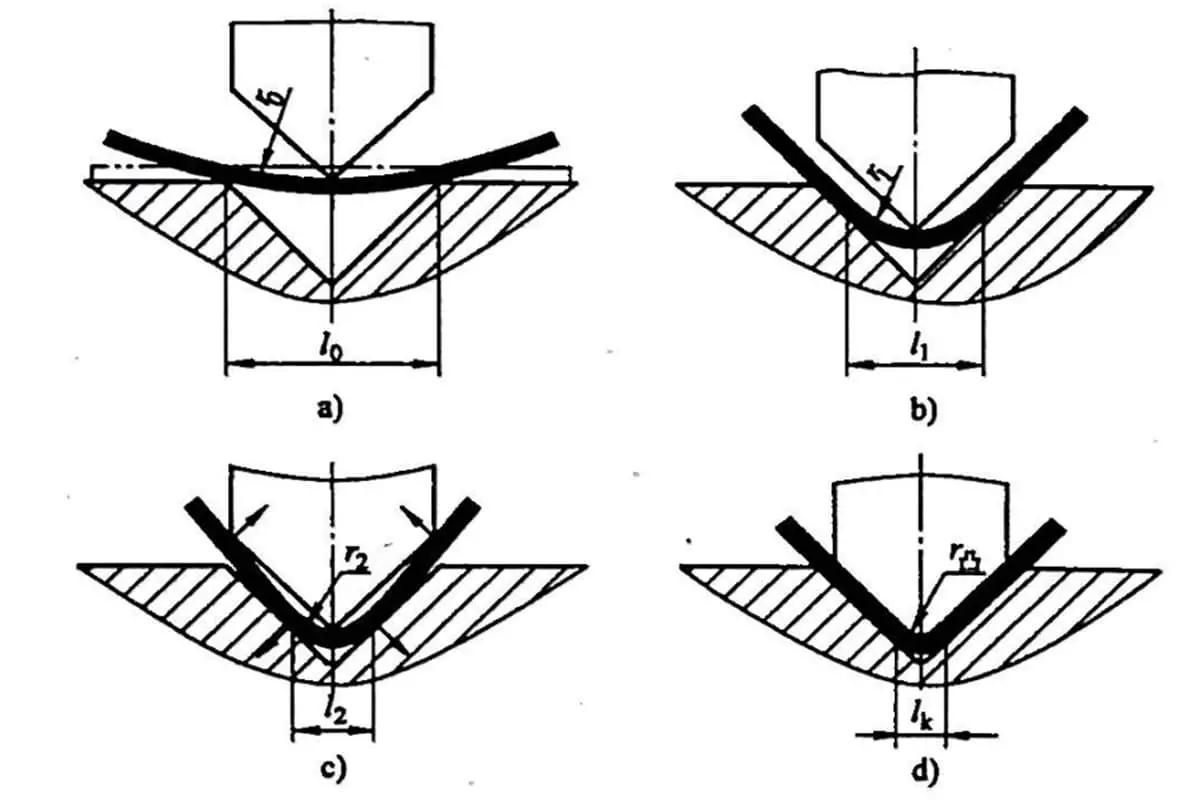
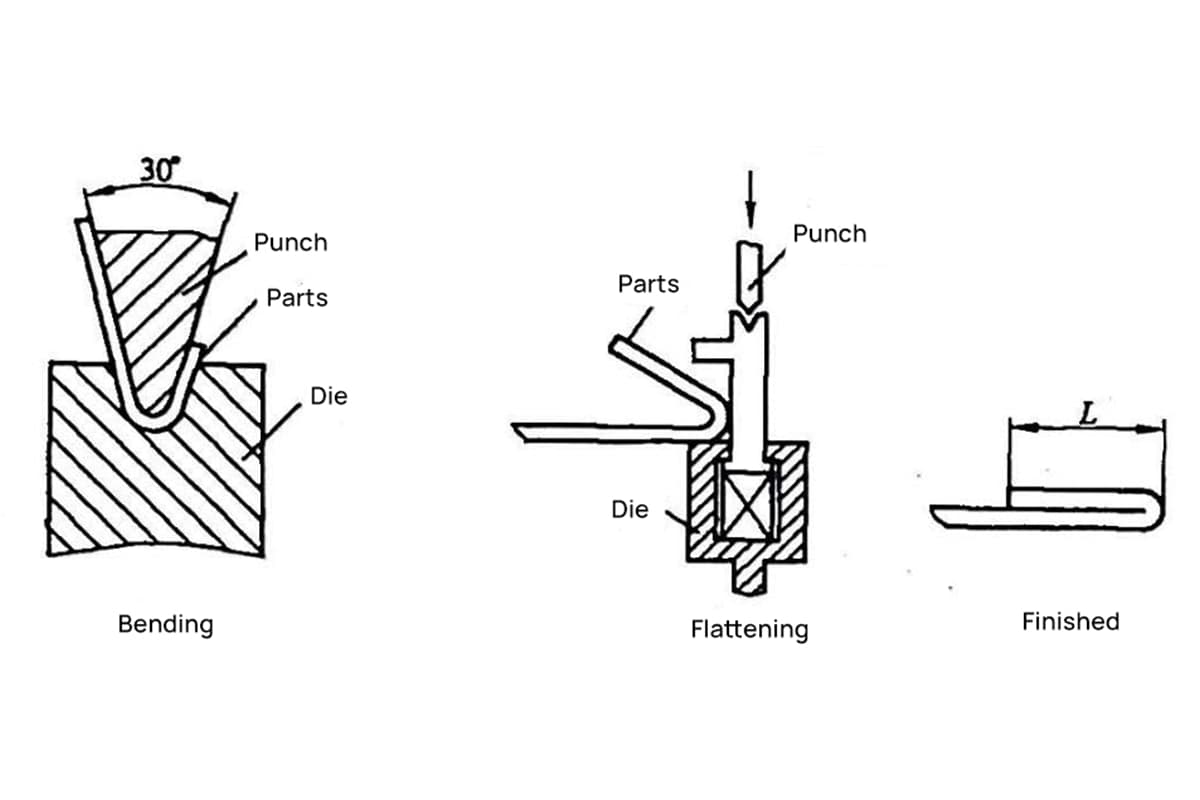
(1) Al aplanar, considere la posibilidad de presionar la línea antes de doblarla en función de las condiciones reales.
El lugar de prensado de la línea se encuentra en el centro de la zona de deformación por flexión.
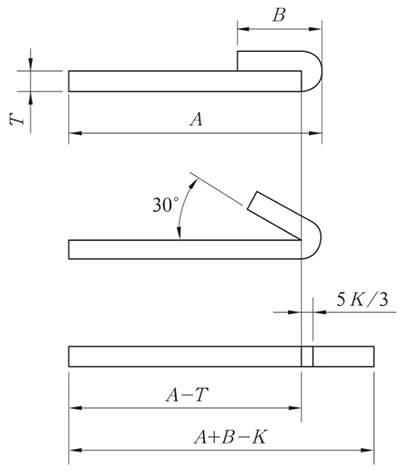
Fig. 9 Diagrama esquemático del plegado y aplanado inversos
Los procesos de plegado inverso y aplanado suelen realizarse en dos pasos: primero, el material se dobla a 30° mediante la matriz de inserción y, a continuación, se aplana.
Por lo tanto, al crear el línea de plegado en el dibujo ampliado, es esencial ilustrar la línea de flexión basada en la flexión de 150°, como se muestra en la figura 9.
Tabla 1 coeficiente de flexión de placas de diferentes espesores bajo diferentes ángulos de flexión
| Ángulo | Espesor/mm | ||||
|---|---|---|---|---|---|
| 1 | 1.2 | 1.5 | 1.8 | 2.5 | |
| 45° | 5.3 | 6.3 | 7.8 | 9.5 | 13 |
| 50° | 4.5 | 5.4 | 6.8 | 8.1 | 11.25 |
| 55° | 4 | 4.7 | 5.8 | 7.05 | 9.75 |
| 60° | 3.4 | 4.1 | 5.1 | 6.15 | 8.5 |
| 65° | 3 | 3.6 | 4.5 | 5.4 | 7.5 |
| 70° | 2.65 | 3.2 | 4 | 4.75 | 6.6 |
| 75° | 2.35 | 2.8 | 3.5 | 4.25 | 5.9 |
| 80° | 2.1 | 2.5 | 3.1 | 3.75 | 5.25 |
| 85° | 1.9 | 2.25 | 2.8 | 3.35 | 4.65 |
| 90° | 1.7 | 2 | 2.5 | 3 | 4.15 |
| 95° | 1.5 | 1.8 | 2.2 | 2.7 | 3.75 |
| 100° | 1.35 | 1.6 | 2 | 2.4 | 3.35 |
| 105° | 1.2 | 1.4 | 1.75 | 2.15 | 3 |
| 110° | 1.1 | 1.3 | 1.6 | 2 | 2.65 |
| 115° | 1 | 1.25 | 1.4 | 1.7 | 2.35 |
| 120° | 0.85 | 1 | 1.25 | 1.5 | 2.1 |
| 125° | 0.75 | 0.9 | 1.1 | 1.35 | 1.85 |
| 130° | 0.65 | 0.8 | 1 | 1.18 | 1.65 |
| 135° | 0.55 | 0.7 | 0.85 | 1.05 | 1.45 |
| 140° | 0.5 | 0.6 | 0.75 | 0.9 | 1.25 |
| 145° | 0.43 | 0.5 | 0.65 | 0.77 | 1.05 |
| 150° | 0.35 | 0.43 | 0.55 | 0.65 | 0.9 |
| 155° | 0.3 | 0.35 | 0.45 | 0.53 | 0.75 |
| 160° | 0.23 | 0.27 | 0.35 | 0.4 | 0.6 |
| 165° | 0.17 | 0.2 | 0.25 | 0.3 | 0.45 |
El método de procesamiento de N pliegues implica tanto la remodelación como el aplanamiento, y el algoritmo para el desdoblamiento es:
L = A + B + K
(K toma la longitud de arco de la capa neutra).
λ = 0,5T
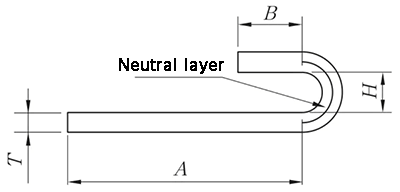
Fig.10 Diagrama de N pliegues
(1) La expansión del arco es directamente K, y se toma la longitud del arco de la capa neutra. λ= 0,5T
(2) Expansión con el borde recto en un lado.
L = A + K
(k es la longitud de arco de la capa neutra)
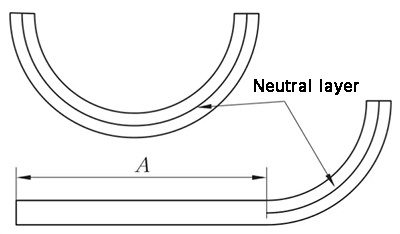
Fig. 11 Diagrama esquemático de la flexión en arco
En la producción real, el control preciso de la longitud desplegada de la chapa mediante software 3D puede lograrse principalmente a través de los siguientes pasos y métodos:
Elija el software de diseño 3D adecuado: En primer lugar, debe elegir un software CAD 3D adecuado para el diseño de chapa metálica. SolidEdge, Creo, FreeCAD, UG, etc. son programas que pueden utilizarse para el diseño de chapa metálica. Estos software proporcionan módulos de chapa metálica o funciones relacionadas que pueden ayudar a los diseñadores con el diseño y los cálculos de despliegue de piezas de chapa metálica.
Utilice el módulo de chapa o las herramientas del software: La mayoría de los programas CAD 3D ofrecen herramientas y funciones relacionadas para el diseño de chapa metálica. Por ejemplo, Creo ofrece una variedad de métodos para controlar las dimensiones desplegadas de la chapa metálica, incluidos los métodos de modelado y despliegue de piezas de chapa metálica de arco grande, método de deducción de curvatura, etc. FreeCAD, como software de modelado 3D de código abierto, también ofrece un módulo de chapa metálica.
Aplicaciónos métodos de cálculo desplegables: Para garantizar la precisión de la longitud una vez desplegada la chapa, se pueden utilizar diferentes métodos de cálculo del desplegado. Entre los métodos más comunes se encuentran el método de compensación de curvatura, el método de deducción de curvatura y el método de cálculo del factor K. Estos métodos pueden ayudar a los diseñadores a calcular la longitud real del material en estado desplegado, garantizando así el tamaño previsto de las piezas tras el plegado y conformado finales.
Preste atención al manejo de bordes y esquinas y al ajuste de detalles: En el proceso de diseño de chapas metálicas, los detalles de manipulación de bordes y esquinas son muy importantes. Algunos programas informáticos, como SW, ofrecen diversas soluciones de manipulación de bordes y esquinas y métodos de plegado, que ayudan a mejorar la precisión del desplegado.
Para las curvas que no sean de 90 grados, los ángulos de curvatura comunes incluyen, entre otros, 45 grados y 135 grados. El método de cálculo del factor K se basa en la relación entre el espesor del material y el radio de curvatura.
En concreto, el factor K = δ / T, donde δ representa el espesor del material y T representa el radio de curvatura. Este método es aplicable para calcular el coeficiente de curvatura de cualquier ángulo que no sea de 90 grados.
En aplicaciones prácticas, debido a las posibles diferencias y grandes errores en los valores de deducción de las curvas en diferentes ángulos, se suele utilizar el factor K como coeficiente de curvatura.
Además, para orientar con precisión el valor del factor K de diferentes espesores de chapa, es necesario realizar ajustes. Algunas referencias sugieren que el valor del factor K para cualquier radio de curvatura puede calcularse mediante técnicas de interpolación específicas, que han demostrado su eficacia en aplicaciones industriales de chapa metálica.
La fórmula de cálculo de la longitud expandida de la chapa plegada biselada es [L = A + B + C + 0,2], donde (A), (B) y (C) representan las dimensiones internas, y 0,2 sirve como valor de compensación.
Basado en los principios y prácticas generales de los cálculos de dilatación de chapas metálicas, este valor de compensación tiene en cuenta las discrepancias entre las longitudes reales y las calculadas teóricamente debido a factores como los errores de flexión del material y de precisión del molde durante las operaciones en el mundo real.
En la transformación de chapa, este valor de compensación contribuye a garantizar la precisión dimensional y la calidad del producto final.
Las piezas de chapa metálica se utilizan mucho en la industria electromecánica, la industria ligera y la automoción.
La forma desplegada de las piezas de chapa metálica es el principal factor determinante del tamaño de la chapa en bruto, que a su vez afecta al tamaño y la forma de la chapa.
Sin embargo, los métodos tradicionales de desplegado de piezas de chapa resultan cada vez más inadecuados para satisfacer las necesidades de diseño modernas debido a sus largos ciclos, su escasa eficacia y su baja calidad.
Para subsanar estas deficiencias, en los últimos años se ha generalizado el uso de sistemas CAD avanzados.
Estos sistemas especializados en el diseño de piezas de chapa metálica cuentan con una sólida funcionalidad y pueden reducir en gran medida la cantidad de tiempo y esfuerzo necesarios para el diseño preliminar y la implantación de piezas de chapa metálica.