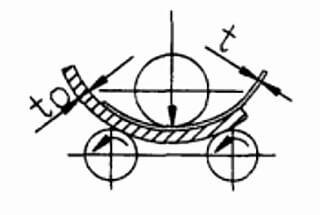
Представьте себе, что вы пытаетесь согнуть толстый стальной лист в идеальный цилиндр - сколько сил вам потребуется? В этой статье мы рассмотрим критические расчеты для определения нагрузки и требуемой мощности для симметричных 3-валковых листогибочных машин. Вы узнаете об анализе усилий, необходимых для проектирования каждой детали, о требованиях к крутящему моменту и мощности, необходимой для системы главного привода. Поняв эти расчеты, вы получите представление о создании эффективных и экономичных листогибочных машин.
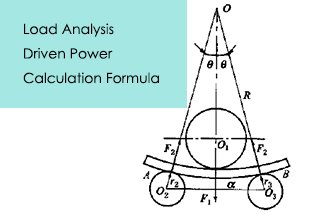
Нагрузка на листогибочные машины значительна, что требует высокой прочности их компонентов. Это необходимо для обеспечения долговечности и производительности машины в тяжелых условиях эксплуатации.
В условиях современной конкуренции снижение стоимости листопрокатных станков имеет решающее значение. Для этого необходимо спроектировать машину с высокой точностью и надежностью, чтобы поддерживать качество и при этом минимизировать расходы.
Для эффективного проектирования валковой гибочной машины необходимо сначала провести всесторонний силовой анализ. Этот анализ позволяет получить фундаментальные параметры, необходимые для проектирования каждой части машины, гарантируя, что все компоненты смогут выдержать эксплуатационные нагрузки, с которыми они столкнутся.
Кроме того, очень важно рассчитать мощность главного привода. Этот расчет имеет решающее значение для проектирования системы главного привода и выбора подходящего двигателя, обеспечивающего эффективную работу машины.
Поэтому проведение детального анализа усилий и точный расчет движущей силы являются важнейшими этапами в процессе проектирования валковой гибочной машины.
В этой статье описывается метод расчета силовых возможностей симметричного трехвалкового гибочного станка. Этот метод также может служить справочным материалом для других типов листогибов прокатные станки, обеспечивая фундаментальный подход к их разработке и оптимизации.
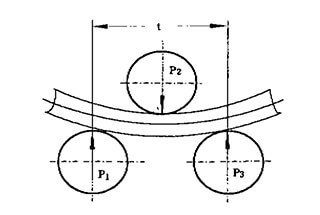
Когда листопрокатный станок работает, стальной лист должен быть закатан в стальную трубу.
В это время напряжение материала достигло предела текучести.
Таким образом, распределение изгибающих напряжений на участке трубы показано на рисунке (b), а изгибающий момент M на участке составляет:
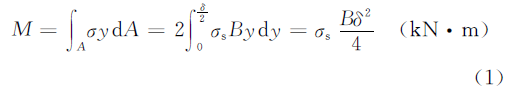
В приведенной выше формуле,
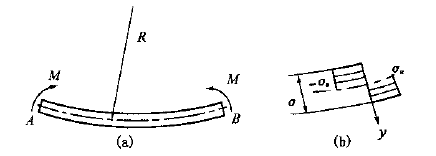
Рис.1 Распределение напряжений при изгибе вала
При рассмотрении деформации материала происходит упрочнение, и для модификации уравнения (1) вводится коэффициент упрочнения K, а именно:
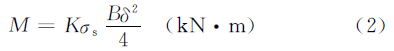
В приведенной выше формуле,
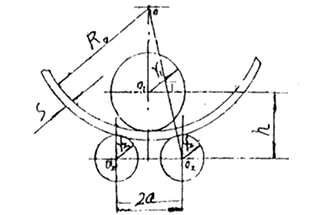
При прокатке стальная пластинаСиловое состояние показано на рисунке ниже. Согласно балансу сил, опорная сила F2 на валковой пластине можно получить по формуле:
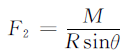
В приведенной выше формуле,
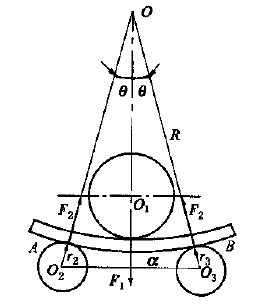
Рис.2 Силовой анализ изгиба вала
Учитывая, что толщина пластины δ намного меньше минимального диаметра прокатной трубы, радиус R нейтрального слоя составляет около 0,5dминДля упрощения расчетов вышеприведенное уравнение можно изменить на:
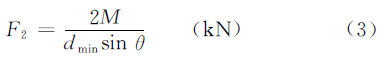
Согласно балансу сил, сила давления F1который генерируется верхним роликом и действует на прокатный лист:
Нижний ролик листопрокатный станок является ведущим роликом, а крутящий момент на нижнем ролике используется для преодоления деформирующего момента Tn1 и момент трения Tn2.
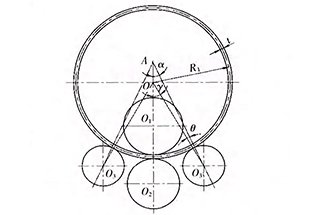
В процессе прокатка стального листаа деформационные возможности, запасенные в сечении AB стального листа (см. рис. 1а и рис. 2), равны 2Mθ, затраченное время составляет 2θR/V (V скорость качения).
Коэффициент равен мощности деформирующего момента Tn1, а именно:
Поэтому,
Момент трения включает в себя момент трения качения между верхним и нижним роликом и стальной пластиной, а также момент трения скольжения между шейкой ролика и втулкой вала, который можно рассчитать следующим образом:
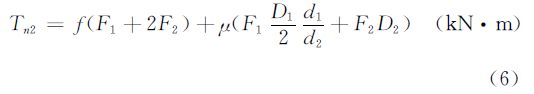
В приведенной выше формуле:
На этапе проектирования размер еще не точен, значение может принимать значение Di = 0.5di (i=1, 2). Крутящий момент привода нижнего ролика T равен сумме деформирующего момента Tn1 и момент трения Tn2.
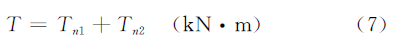
Мощность привода нижнего ролика:
В приведенной выше формуле:
Мощность главного двигателя можно определить по значению P.
Как основатель MachineMFG, я посвятил более десяти лет своей карьеры металлообрабатывающей промышленности. Мой обширный опыт позволил мне стать экспертом в области производства листового металла, механической обработки, машиностроения и станков для обработки металлов. Я постоянно думаю, читаю и пишу об этих предметах, постоянно стремясь оставаться на переднем крае своей области. Позвольте моим знаниям и опыту стать преимуществом для вашего бизнеса.
RU 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
KO