Bearing Life Calculation: The Secrets of Predicting Bearing Life

Practical Calculation of Bearing Lifespan

Previously, we have discussed how to calculate the lifespan of a bearing. In those articles, we mainly introduced the theoretical aspects of bearing lifespan and the calculation formula.

Today, we aim to apply that theory to practical scenarios. After all, the ultimate goal of gaining theoretical knowledge is to serve practical engineering needs. Some engineers have requested real-world calculation examples, so let’s delve deeper using the example from our previous article.

Let’s revisit the example of the vertical motor. Here are the relevant bearing details:

• Bearing model: 6208
• Basic dynamic load rating of the bearing: 29kN
• Equivalent dynamic load of the bearing: P=5.83kN

Let’s also provide some additional parameters for this bearing:
Bearing speed: n=1500rpm

Using the bearing life formula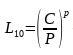we obtain the lifespan of the bearing:

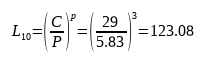
Here, p is the calculation coefficient for the bearing. When the rolling element of the bearing is a ball, p is 3, and when the rolling element is a roller, p is 10/3. The resulting bearing life is 123.08, in million revolutions. Converted to a more common time unit, we get:

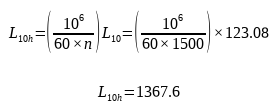
The calculated bearing life is approximately 1368 hours.

In this example, we used a scenario where the bearing is under a high load. The calculated result suggests that the bearing is not suitable for this application due to its short lifespan. If the motor operates continuously, the basic rated life can only assure less than two months of bearing operation.

That is to say, if we choose this bearing, we can only guarantee that 90% of the bearings can operate continuously for two months under these conditions.

The above is the bearing life value obtained using basic bearing life theory.

However, as you may have noticed, just like in our previous articles, the entire calculation process only considers the load on the bearing. In other words, this so-called rated bearing life only considers the impact of the load. As we discussed in our previous articles, after many years of development in modern bearing life theory, this calculation no longer meets our needs. Therefore, we need to further adjust this value.

That is, we need to calculate the modified life value of the bearing. Most of the subsequent calculations do not use formulaic methods because these calculations can be complex, many of the processes or reference theories come from experiments, and thirdly, various bearing suppliers and international bearing standards have provided us with a better reference tool – charts. So, how do we use these charts? Let’s explore this using our example.

Adjusted Rating Life of Bearings

As outlined in our previous articles, the formula for the adjusted life is as follows:

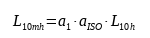
To determine the final value L_10mh we need to define a1 and a_iso.

01 Firstly, we define a1.

As we have previously discussed, a1 is known as the reliability coefficient of the adjusted life. When the reliability is 90%, the value of a1 is 1. For general-purpose machinery used in industry, unless specifically required, the life of the bearing is always based on a 90% reliability. Therefore, in this example, we can directly take a1.

02 Secondly, we find a_iso.

The standard method for calculating the adjusted life coefficient a_iso of a bearing considers the following factors:

• Bearing load
• Lubrication conditions (type and viscosity of lubricant, speed, bearing size, whether additives are used)
• Fatigue limit of the bearing
• Type of bearing
• Residual stress of the bearing
• Environmental conditions
• Contamination in the lubricant

In summary, a_iso is a function of the following parameters:

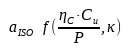
Where:

• η_c is the contamination factor of the bearing,
• C_u is the fatigue load limit of the bearing,
• k is the viscosity ratio of the bearing lubricant.

First, we select the contamination factor ηc of the bearing. In the ISO281 standard and all bearing manufacturer catalogs, there is a reference table for selection criteria as follows:

In the application of vertical motors, based on our previous experience, the contamination factor for bearings should be selected between light pollution and general cleanliness. In this case, we choose a contamination factor of 0.6, which is slightly higher than general cleanliness.

Let me add,

The selection of the contamination factor does not have a specific mathematical formula to refer to. It generally relies on years of bearing application experience. The more applications we encounter, the more insights we gain in this selection.

Since the selected bearing is 6208, the fatigue load limit C_u of this bearing can be found in the bearing catalog as: 1.05kN

The equivalent dynamic load value of the bearing was calculated in the previous chapter to be P=5.83kN

Therefore, we can obtain an approximate value:

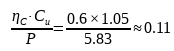
Next, we need to make a slightly more complex choice of viscosity ratio k. Due to the limited space in this chapter, we won’t elaborate on the specific meaning of k and how to choose this value. We will write another article to detail it later. For now, we only want to emphasize that for bearings, choosing the right lubrication is very important. This not only relates to the quality of the grease itself but also to the impact of lubrication on the bearings.

Regarding the viscosity ratio,

Generally, we hope that the final chosen lubrication value of k can be selected between 1 and 4, with several considerations.

If the calculated k value of the selected lubrication value is:

• Less than 1, it means that the lubrication has not achieved the desired effect. The purpose of a lubricant is to separate the steel-to-steel contact between the bearing raceway and the rolling element. If k<1, it indicates that the lubricant has not separated the steel-to-steel contact, and the bearing will still generate friction when it runs.
• Greater than 4, it means that too much lubricant has been added. Although it perfectly separates the metal contact, the excessive lubricant in the bearing will generate what we call “drag loss” torque. This is a very important part of the bearing friction model. In layman’s terms, the main purpose of lubrication is to reduce friction and further lower the temperature of the bearing. However, too much lubricant can also generate “friction,” which will also generate heat.

Therefore, we have selected a suitable lubrication value, and the final k value is 1.5.

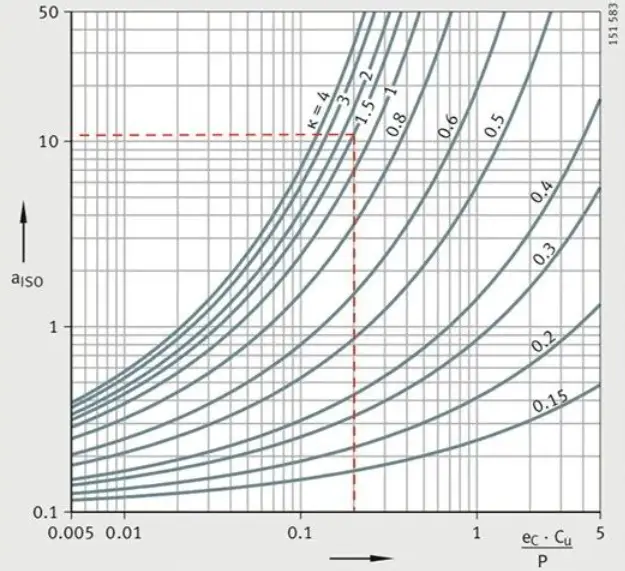
With these two parameters, we can find the following chart in ISO281 or the bearing manufacturer’s catalog.

Caution!

There are several similar diagrams, each for different types of bearings. We’ve chosen the deep groove ball bearing, which is a type of radial ball bearing. Therefore, select the appropriate chart based on the specific type of bearing.

From the chosen diagram, we can determine that, under this application, aiso=12.

In this example, the final corrected rated life of bearing 6208 is:

L_10mh = a₁×a_iso×L_10h = 1×12×1367.6 = 16411.2

In this vertical motor, under proper lubrication conditions, the bearing can ultimately operate for 16,410 hours.

Purpose of The Calculation

Since the result of bearing life calculation cannot accurately reflect the actual life of the bearing, what is the purpose of this calculation?

In fact, many engineers misunderstand lifespan calculation as “fortune-telling,” likely due to its name. Originally, the aim of studying bearing fatigue life was to establish a reference value, a lifespan reference. Over time, this reference value has become a parameter for comparing and verifying the reasonableness of bearing selection.

In fact, bearing life calculation is a check on the load capacity of the chosen bearing. In other words, it’s about choosing the smallest bearing that can meet the lifespan requirement. In this sense, the calculation of bearing life is a requirement for the lower limit of bearing load capacity.

How can we understand this? Let’s start from the process of life check:

When engineers verify the life of bearings, mechanical design manuals and equipment materials always provide some minimum values for life requirements. The following is one example:

Certainly, some equipment manufacturers provide different lifespan requirements. Often, these lifespan values are met by the bearings in traditional designs.

Thus, when designing new equipment and verifying the bearing lifespan, the following approach can be used:

• If the lifespan of the newly chosen bearing is less than the required lifespan: The load capacity (and corresponding lifespan under this load) of the selected bearing is less than that of the bearings that have previously satisfied this condition. In other words, the bearing chosen is too small;
• If the calculated lifespan of the newly chosen bearing is greater than or equal to the required lifespan: The load capacity (and corresponding lifespan under this load) of the selected bearing is greater than that of the bearings that have previously satisfied this condition. In other words, the bearing chosen is too large;

Choosing too small or too large should be within a reasonable range, and absolute equality should not be pursued. Therefore, when observing the “required lifespan,” one would find that this value is a range, not an absolute.

Therefore, the implicit calculation of bearing life involves verifying the bearing’s load capacity under reasonable lifespan requirements. In other words, choose a bearing of reasonable size under given working conditions.

In real life, due to misunderstandings of the above concepts, many “misoperations” occur:

(1) The calculated lifespan of a bearing must meet the warranty period of the equipment.

This practice confuses the bearing load check with the equipment’s lifespan. In fact, a bearing’s life check is not equivalent to “fortune-telling,” as explained in the previous article.

The actual bearing conditions are varied, and engineers cannot calculate each machine individually. This is a misunderstanding by equipment manufacturers about “bearing life calculation.”

The concept of a warranty period places all responsibility on the equipment manufacturer, a “warranty” concept that is much broader than the concept covered by “bearing life calculation,” making such a direct application inappropriate.

Of course, some engineers, due to the pressure from the client, are forced to meet a “20-year” lifespan requirement. Under such a mandate, the chosen bearings are often oversized, which not only results in economic inefficiency but also misunderstands that bigger or longer life calculations are not always better for bearings.

(2) The longer the calculated lifespan of a bearing, the better it sounds.

In fact, this also misleads the selection of bearings. As I mentioned earlier, the bearing life check calculation is a check of the minimum load capacity of bearings under working conditions.

On the other hand, there should also be a limit to the maximum load capacity of bearings, which is the upper limit of the load capacity of bearings under working conditions. If the calculation result exceeds this value, problems will occur with the bearing.

This is what we often refer to as the “minimum load of the bearing.” If the chosen bearing is too large, and the calculated lifespan of the bearing under working conditions is long, which means the bearing’s load capacity is very high, it may not meet the minimum load requirement of the bearing.

If the load borne by the bearing is less than the required minimum load, issues like rolling element slippage may occur inside the bearing, making it more prone to burning out.

Indeed, understanding the concept of bearing life can lead to numerous optimizations in design. These include:

Assessing whether it’s possible to reduce the size of the bearing while meeting lifespan requirements;

Keeping a record of the lifespan of numerous bearings, and considering further size reduction if there’s consistently some residual life.

In summary, in engineering practice, bearing life calculation is used to verify the bearing’s load capacity, not to simply maximize it. Moreover, this calculated life does not reflect the “true” lifespan of the bearing.

A precise understanding of bearing life concepts aids in the correct selection of bearing sizes.

Regrettably, in actual work, we sometimes have to submit to the demands of our clients, even if we believe their requests are technically unreasonable. Therefore, feel free to share this article with them.

This might be the most challenging article to understand on the website so far, especially for electrical engineers. If anyone has any questions, feel free to leave a comment for discussion.