Вы когда-нибудь задумывались, как конструкторы листового металла обеспечивают точность своих проектов? В этой статье блога мы погрузимся в увлекательный мир проектирования листового металла и изучим два важнейших понятия: припуск на изгиб и вычет на изгиб. Мы также познакомимся с коэффициентом K и его ролью в расчетах. Присоединяйтесь к нам, чтобы раскрыть эти темы и получить ценную информацию от экспертов отрасли.
В области проектирования листового металла часто можно услышать такие термины, как припуск на изгиб, вычет на изгиб и коэффициент K. Но что именно означают эти термины? И как их рассчитать?
В этом посте мы дадим подробные ответы на эти вопросы.
Инженеры и продавцы, занимающиеся разработкой и производством листовой металл детали используют различные алгоритмы для расчета фактической длины материала в развернутом состоянии, чтобы обеспечить требуемые размеры детали после окончательной гибки и формовки.
Наиболее часто используемым методом является простое "правило защемления пальцев" - алгоритм, основанный на личном опыте, который учитывает такие факторы, как тип и толщина материала, радиус и угол изгиба, тип станка и скорость гибки.
С развитием компьютерных технологий автоматизированное проектирование (CAD) все чаще используется для использования преимуществ аналитических и вычислительных способностей компьютера.
Однако даже если компьютерная программа моделирует сгибание или разгибание листового металла, ей все равно необходим метод точного расчета.
Большинство коммерческих систем автоматизированного проектирования и трехмерного твердотельного моделирования предоставляют общее и мощное решение для этого, и, как правило, они совместимы с оригинальным методом "пальцевых правил" и предлагают возможности настройки для ввода специфического содержимого в процесс расчета.
SolidWorks является лидером в предоставлении таких возможностей для конструкция из листового металла.
В заключение следует отметить, что в настоящее время широко распространены два популярных алгоритма гибки листового металла: один основан на припуск на изгиб, а другой - на основе вычитания изгиба.
Чтобы расширить представление читателей об основных понятиях в конструкция из листового металла расчеты, будут обобщены и объяснены следующие моменты:
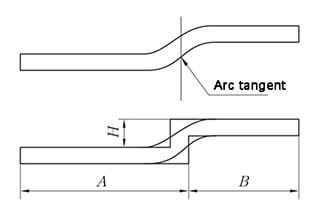
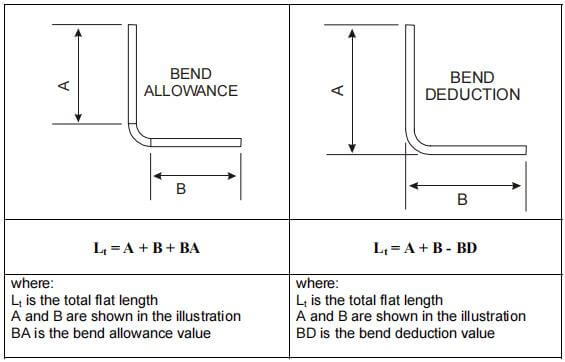
Для более четкого понимания припуск на изгибОбратитесь к рисунку 1, на котором показан один изгиб детали из листового металла. На рисунке 2 показана деталь в развернутом состоянии.
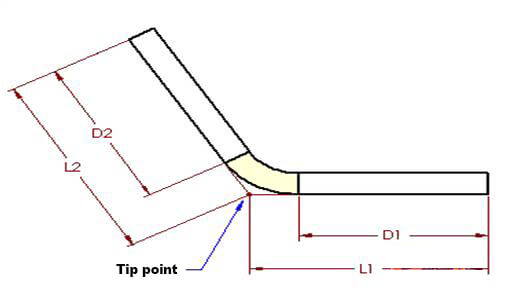
Рисунок 1
Рисунок 2
Алгоритм определения припусков на изгиб описывает развернутую длину (LT) детали из листового металла как сумму длин каждого сегмента после сплющивания детали плюс длина области сплющенного изгиба.
Сайт припуск на изгиб (BA) представляет собой длину области плоского изгиба. Таким образом, общая длина детали может быть выражена в виде уравнения (1):
LT = D1 + D2 + BA (1)
Область изгиба (на рисунке показана светло-желтым цветом) - это область, которая теоретически подвергается деформации в процессе изгиба.
Чтобы определить геометрию развернутой детали, выполните следующие действия:
Задача определения длины плоского участка изгиба, представленного на рисунке символом BA, немного сложнее.
Значение BA зависит от таких факторов, как тип материала, толщина материала, радиус изгиба и угол, а также процесс гибки, тип станка и его скорость.
Значение BA может быть получено из различных источников, включая поставщиков листового металла, экспериментальные данные, опыт и инженерные руководства.
В SolidWorks можно напрямую ввести значения BA или использовать коэффициент K (который будет рассмотрен позже) для расчета значений.
Сайт гибочный стол Метод является наиболее точным способом определения различных припусков на изгиб для различных ситуаций с разными толщинами, радиусами и углами.
Создание первоначального гибочного стола может занять некоторое время, но после того, как он будет сформирован, его части можно будет использовать повторно в будущем.
Для каждого изгиба детали может быть введена одинаковая или разная информация.
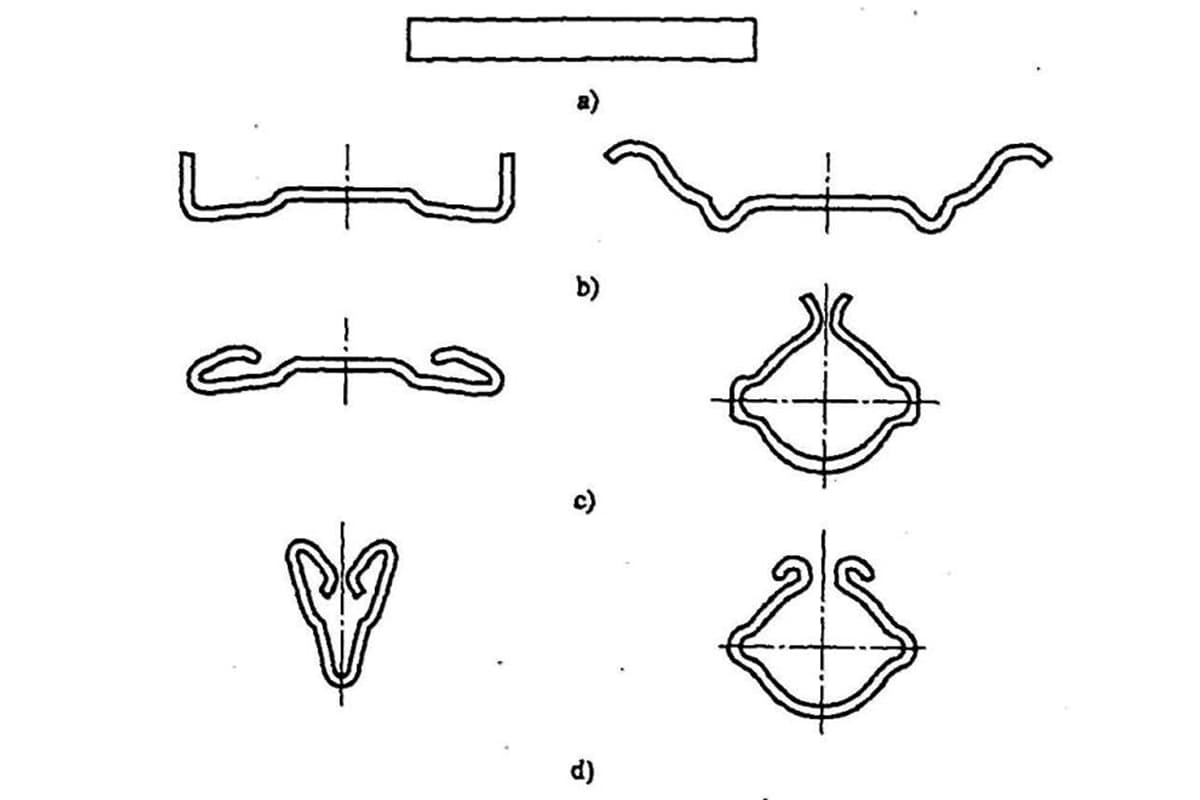
1) Стандарты для общих изгибов
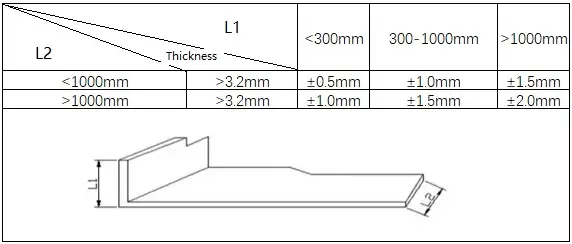
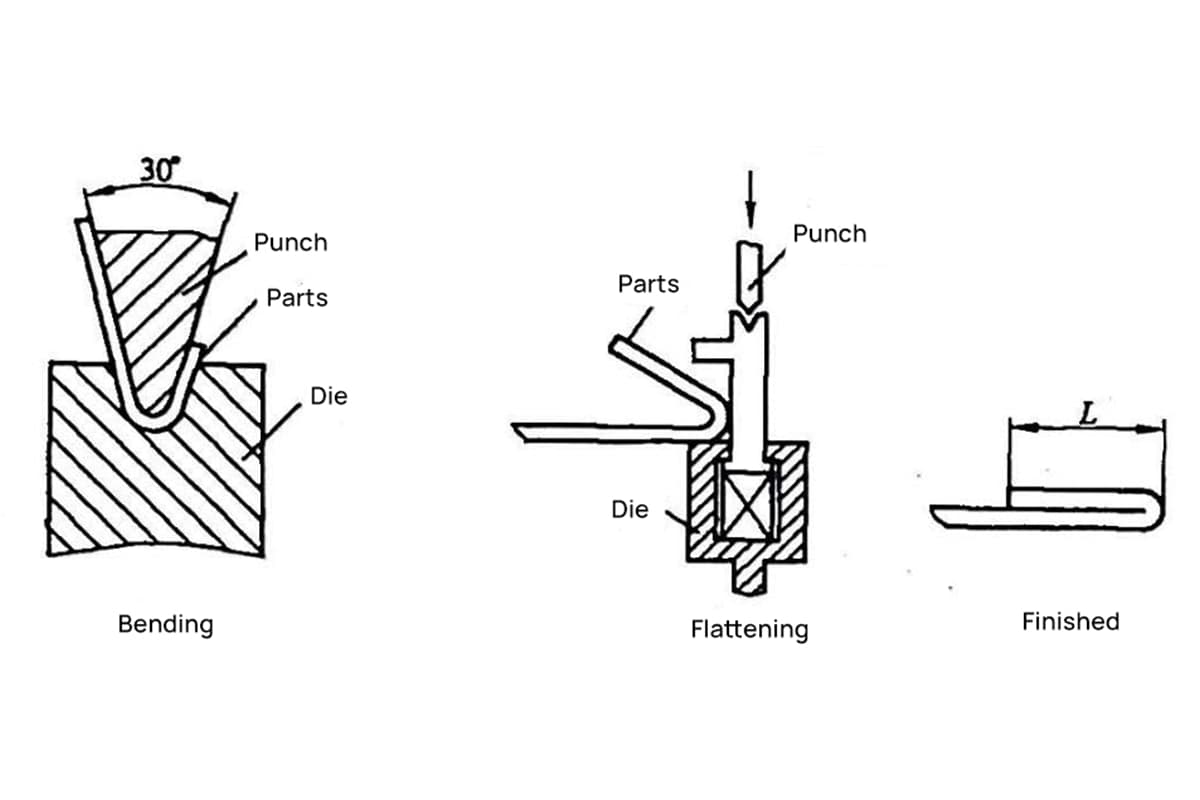
2) Стандарты для Z-образной гибки
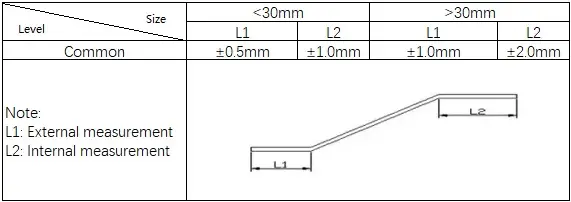
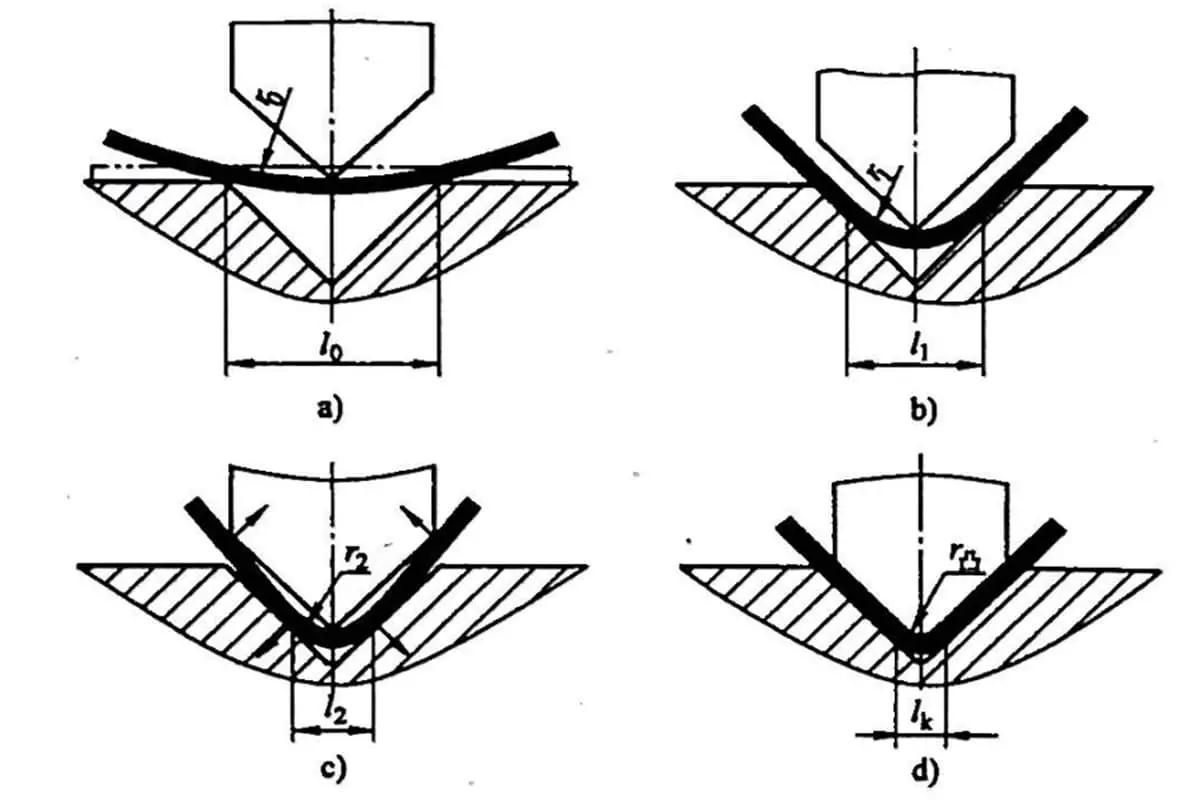
3) Стандарты для V-образной гибки
4) Стандарты для U-образный изгиб
Похожие статьи: Калькулятор силы V- и U-образного изгиба
Сгибание Вычитание - это термин, используемый для описания величины отката в процессе гибка листового металла. Это еще один простой алгоритм для описания процесса.
Рисунки 1 и 2 также относятся к этой концепции. Согласно методу вычитания изгиба, уплощенная длина (LT) детали равна сумме длин двух плоских участков, простирающихся до "точки вершины" (гипотетического пересечения двух плоских участков), за вычетом вычитания изгиба (BD).
Таким образом, общая длина детали может быть выражена как показано в уравнении (2):
LT = L1 + L2 - BD (2)
Значение BD может быть определено или получено из различных источников, таких как лист металлический материал поставщики, экспериментальные данные, опыт, инженерные справочники с уравнениями или таблицами и т.д.
Рисунок 3
Пользователям, знакомым с методом вычитания изгиба, важно понимать взаимосвязь с методом припуска на изгиб, который широко используется в SolidWorks.
Связь между этими двумя величинами можно легко вывести, используя две геометрии сгибания и разгибания деталей.
Сравнивая уравнения (1) и (2), получаем:
LT = D1 + D2 + BA (1) LT = L1 + L2 - BD (2)
И поэтому,
D1 + D2 + BA = L1 + L2 - BD (3)
На рисунке 3 угол A представляет собой угол изгиба, который описывает угол, пройденный деталью при изгибе, а также угол дуги, образованной зоной изгиба, которая показана в виде двух половин.
Используя размеры и принципы построения правильных треугольников, мы можем вывести следующие уравнения:
D1 = L1 - (R + T)TAN(A/2) (4) D2 = L2 - (R + T)TAN(A/2) (5)
Подставив уравнения (4) и (5) в уравнение (3), мы можем получить зависимость между BA и BD:
BA = 2(R + T)TAN(A/2) - BD (6)
А когда угол изгиба равен 90 градусам, это уравнение упрощается до:
BA = 2(R + T) - BD (7)
Эти уравнения (6) и (7) обеспечивают удобный метод преобразования из одного алгоритма в другой, используя в качестве параметров только толщину материала, угол/радиус изгиба и т.д.
Для пользователей SolidWorks эти уравнения представляют собой прямой метод преобразования вычета на изгиб в припуск на изгиб.
Значение параметра "Допуск на изгиб" может использоваться для всей детали или каждого отдельного изгиба, а также может быть включено в таблицу данных по изгибу.
Коэффициент K - это отдельная величина, которая объясняет изгиб и разгибание листового металла в различных геометрических сценариях.
Это также автономное значение, которое используется для расчета припуска на изгиб (BA) при различных условиях, таких как толщина материала, углы изгиба и радиусы.
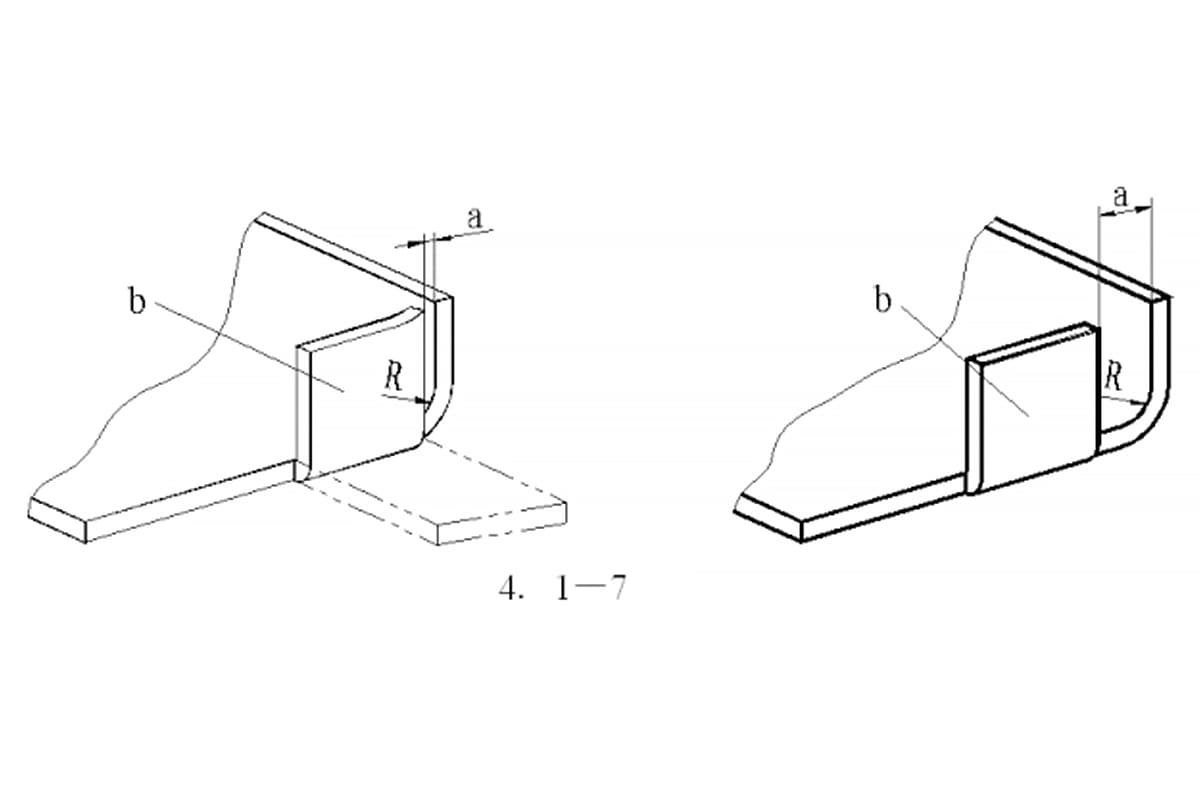
Рисунки 4 и 5 приведены для того, чтобы помочь прояснить углубленное определение коэффициента K.
Рисунок 4
Рисунок 5
Мы можем подтвердить наличие нейтральной оси в толщине металлического листа. Лист металлический материал нейтральная ось в области изгиба не растягивается и не сжимается, то есть это единственная область, которая не деформируется при изгибе.
На рисунках 4 и 5 показана граница между розовой и голубой областями.
При изгибе розовая область сжимается, а синяя - растягивается. Если нейтральный слой листового металла остается недеформированным, длина его дуги в области изгиба остается одинаковой независимо от того, согнута деталь или сплющена.
В результате припуск на изгиб (BA) должен быть равен длине дуги нейтрального слоя в области изгиба детали из листового металла, которая показана зеленым цветом на рисунке 4.
Положение нейтрального слоя металлического листа зависит от свойств конкретного материала, например, от его пластичности.
Предполагается, что расстояние между нейтральным слоем листового металла и поверхностью равно "t", или глубине от поверхности листовой детали в материал в направлении толщины.
В результате радиус дуги нейтрального слоя можно выразить как (R + t). Используя это выражение и угол изгиба, можно рассчитать длину дуги нейтрального слоя (BA).
BA = Pi(R+T)A/180
Чтобы упростить определение нейтрального слоя листового металла и сделать его применимым ко всем материалам, было введено понятие коэффициента K.
Определение коэффициента K таково: это отношение толщины нейтрального слоя листового металла к общей толщине материала детали из листового металла. Другими словами, коэффициент K определяется как:
K = t/T
Поэтому значение K всегда будет находиться в диапазоне от 0 до 1. Если коэффициент K равен 0,25, это означает, что нейтральный слой расположен на уровне 25% от общей толщины листового материала.
Аналогично, если он равен 0,5, это означает, что нейтральный слой расположен на 50% всей толщины, и так далее.
Объединив вышеуказанные уравнения, можно получить следующее уравнение (8):
BA = Pi(R+K*T)A/180 (8)
Поэтому значение K всегда будет находиться в диапазоне от 0 до 1.
Если коэффициент K равен 0,25, это означает, что нейтральный слой расположен на расстоянии 25% от толщины материала листового металла детали.
Аналогично, если он равен 0,5, это означает, что нейтральный слой расположен на расстоянии 50% от всей толщины, и так далее.
Происхождение коэффициента K можно проследить в традиционных источниках, таких как поставщики листового металла, данные испытаний, опыт, руководства и т.д.
Однако в некоторых случаях предоставляемая ценность не может быть выражена в виде четкого коэффициента K, но все же можно найти взаимосвязь между ними.
Например, если в руководстве или литературе нейтральная ось описана как "расположенная на расстоянии 0,445x толщины материала от поверхности листа", это можно интерпретировать как коэффициент K, равный 0,445, то есть k = 0,445.
Подставив это значение K в уравнение (8), можно получить следующую формулу.
BA = A (0,01745R + 0,00778T)
Если уравнение (8) модифицировать другим методом, вычислить константу в уравнении (8) и сохранить все переменные, то можно получить следующее:
BA = A (0,01745 R + 0,01745 K*T)
Сравнивая эти два уравнения, легко определить, что 0,01745 * k = 0,00778, и, следовательно, k может быть рассчитан как 0,445.
Выяснилось, что в системе SolidWorks также предусмотрен алгоритм расчета припусков на изгиб для определенных материалов, когда угол изгиба составляет 90 градусов. Формула расчета для каждого материала выглядит следующим образом:
На самом деле, упростив уравнение (7) и установив угол изгиба в 90 градусов, можно вычислить константу и преобразовать уравнение следующим образом:
BA = (1,57 * K * T) + (1,57 *R)
Таким образом, сравнивая вышеприведенную формулу расчета, значение K для материалов из мягкой латуни или мягкой меди может быть получено как 1,57xk = 0,55, или K = 0,35.
Используя тот же метод, можно легко рассчитать значения коэффициента K для нескольких типов материалов, перечисленных выше.
Как уже говорилось, существует несколько источников, из которых можно получить значение коэффициента K, например, поставщики материалов, данные испытаний, опыт и руководства.
Чтобы создать точную модель из листового металла с помощью метода K-фактора, очень важно найти подходящий источник K-фактора, отвечающий вашим инженерным требованиям. Это обеспечит требуемую точность результатов изготовления физической детали.
В некоторых ситуациях невозможно получить точные результаты, используя только одно значение коэффициента K, особенно если необходимо учесть широкий спектр сценариев изгиба.
В таких случаях рекомендуется использовать значение припуска на изгиб (BA) непосредственно для одного изгиба всей детали или использовать таблицу изгибов для описания различных значений BA, вычета на изгиб (BD) или коэффициента K, соответствующих различным значениям A, R и T во всем диапазоне.
Кроме того, уравнения можно использовать для генерации данных, как в примере таблицы изгибов, предоставленной SolidWorks. При необходимости ячейки таблицы изгибов можно также изменить на основе экспериментальных или эмпирических данных.
В каталог установки SolidWorks включены таблицы припусков на изгиб, таблицы вычетов на изгиб и таблицы коэффициентов K, которые можно редактировать и настраивать по мере необходимости.
В этом посте представлен полный обзор распространенных методов расчета и лежащих в их основе принципов, используемых при проектировании и изготовлении деталей из листового металла.
В нем рассматривается расчет припусков на изгиб, вычетов на изгиб и коэффициентов K, а также объясняются различия между этими методами и их взаимосвязь.
Она служит полезным справочником для инженеров и технических специалистов отрасли.
Примечание:
Как основатель MachineMFG, я посвятил более десяти лет своей карьеры металлообрабатывающей промышленности. Мой обширный опыт позволил мне стать экспертом в области производства листового металла, механической обработки, машиностроения и станков для обработки металлов. Я постоянно думаю, читаю и пишу об этих предметах, постоянно стремясь оставаться на переднем крае своей области. Позвольте моим знаниям и опыту стать преимуществом для вашего бизнеса.
RU 
EN 
DE 
ES 
FR 
IT 
NL 
PT 