How do engineers predict when a material will fail under repeated stress? This article introduces the S-N curve, a key tool in fatigue analysis. You’ll learn how average stress, multiaxial stress conversion, and irregular stress are treated to predict material fatigue life. Understanding these concepts can help in designing more durable and reliable components. Read on to explore the intricacies of fatigue analysis and ensure the longevity of your engineering projects.
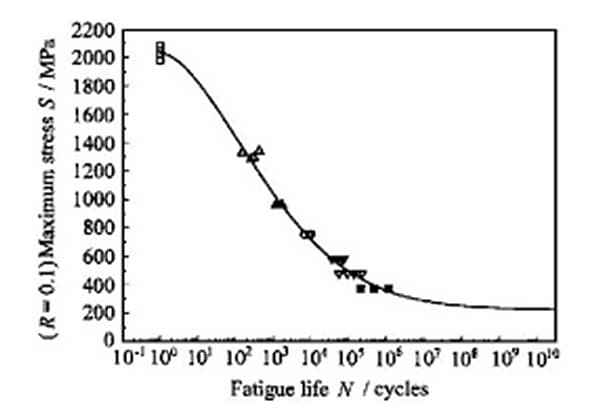
The fatigue properties of materials are typically expressed through uniaxial stress cycles, known as S-N curves. It’s important to note that fatigue theory based on fracture mechanics is not being considered in this context.
The stress variation over time often follows a regular pattern, such as a sine wave, square wave, or pulse. However, the influence of average stress on fatigue performance is often disregarded (i.e., the impact of r=Smin/Smax ≠ -1).
In reality, stress state is usually multiaxial, with an irregular stress variation and r≠-1. The correspondence between actual stress and fatigue performance measured in the lab, which involves regular stress variation, uniaxial stress, and r=1, forms the basis for fatigue analysis.
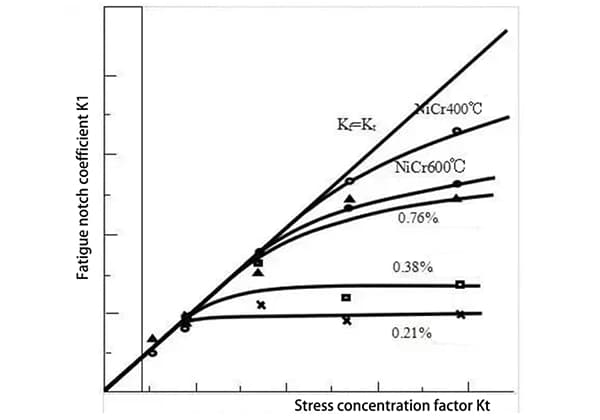
When there are S-N curves available for different r values, the interpolation method is typically employed to determine the S-N curve for unknown r values.
In cases where only an S-N curve with r=-1 is available, the following formula can be utilized to calculate the equivalent stress. This formula converts the uniaxial stress of r≠-1 to the uniaxial stress when r=-1, which is known as the equivalent stress:
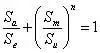
Where, Sa is the half stress amplitude, Se is the desired equivalent stress, Sm is the average stress, and different values of Su and n constitute different theories:
The following stress options are available to determine the type of stress used for the transformation: Von Mises equivalent stress, maximum shear stress, maximum principal stress, or a specific stress component (such as Sx, Syz, etc.).
Sometimes, Mises stress with a sign is also employed, with its magnitude remaining unchanged. The sign corresponds to the sign of the maximum principal stress. One advantage of this method is that it allows for the consideration of tension or compression effects, which are reflected in the average stress or r.
Similar to the strength theory, Von Mises equivalent stress and maximum shear stress conversion are suitable for materials with high ductility, while the maximum principal stress conversion is appropriate for brittle materials.
The equivalent uniaxial stress time curve of irregular high and low is analyzed to extract a series of simple stress cycles (Sa, Sm) and their corresponding times.
Counting and statistics can be achieved using various methods, including the path dependent method and the path independent method.
The path correlation method, which is the most widely used rain flow counting method, is applied to complete the counting process. Its algorithm and principle are explained in “Downing, S., Society, D. (1982) Simplified rain flow counting algorithms. Int J Fatigue, 4, 31 – 40”.
After the rain flow treatment, the irregular stress time curve is transformed into a series of simple cycles (Sa, Sm, and ni, where ni is the number of cycles).
This method allows for the application of the damage accumulation theory (Miner criterion) to calculate and analyze: Sum (ni/Ni), where Ni is the life corresponding to the stress cycle (considering Sa, Sm, see above).
This technique is commonly used to measure the safety factor after a certain number of cycles or the corresponding life of a specific complex stress cycle.
At present, commercial fatigue analysis software is mostly based on the aforementioned process.
However, it should be noted that fatigue analysis is an empirical analysis, and a mature and complete theory does not currently exist.
There are varying perspectives regarding the conversion of multiaxial stress to uniaxial stress.
The Von Mises stress, for instance, is a stress dimension quantity based on the idea of the specific energy of shape change.
Using the concepts of positive and negative or tension and compression is an imprecise method, and it is not recommended.
The selection of stress type to adopt depends on the possible trend of cracks on materials or structures to determine which kind of stress is the primary factor controlling fatigue failure.
Engineering practice has shown that steel with good plasticity is often damaged due to repeated dynamic loading of principal stress in cases of fatigue failure.
Supplement on the Treatment of Average Stress Effect:
“If there are S-N curves under different R values, the interpolation method is generally used to determine the S-N curve under unknown R values.”
This is only one method, which is useful when there are multiple stresses to check. However, this method can be cumbersome when checking only one stress life.
Another method is to determine the equivalent stress half amplitude under the condition of R = -1, and then apply the S-N curve directly.
When there is a mean stress, the S-N curve cannot be used directly. Instead, use the GOODMAN CURVE or the modified GOODMAN CURVE.
As the founder of MachineMFG, I have dedicated over a decade of my career to the metalworking industry. My extensive experience has allowed me to become an expert in the fields of sheet metal fabrication, machining, mechanical engineering, and machine tools for metals. I am constantly thinking, reading, and writing about these subjects, constantly striving to stay at the forefront of my field. Let my knowledge and expertise be an asset to your business.
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO