Ever wondered how materials fail under stress? The Four Strength Theory unravels this mystery, explaining how different forces lead to fractures or yielding. This article explores maximum tensile stress, elongation strain, shear stress, and specific energy of shape change theories, shedding light on their applications and limitations. By reading, you’ll understand how to predict and prevent material failure in various engineering contexts.
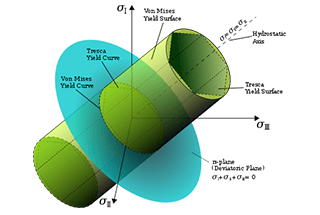
This theory is commonly referred to as the first strength theory. It holds that the primary cause of failure is the maximum tensile stress. If the first principal stress reaches the uniaxial tensile strength limit, regardless of the complexity or simplicity of the stress state, it results in fracture.
Failure form: Fracture
Damage conditions: σ1 =σb
Strength condition: σ1≤[σ]
Experiments have shown that this strength theory can better explain the fracture phenomenon of brittle materials such as stone and cast iron, particularly in areas where the maximum tensile stress is located. However, it is not suitable for cases without tensile stress, such as one-way compression or three-way compression.
Disadvantage: It does not consider the other two principal stresses.
Scope of application: This theory is suitable for the tension of brittle materials, such as the stretching and twisting of cast iron.
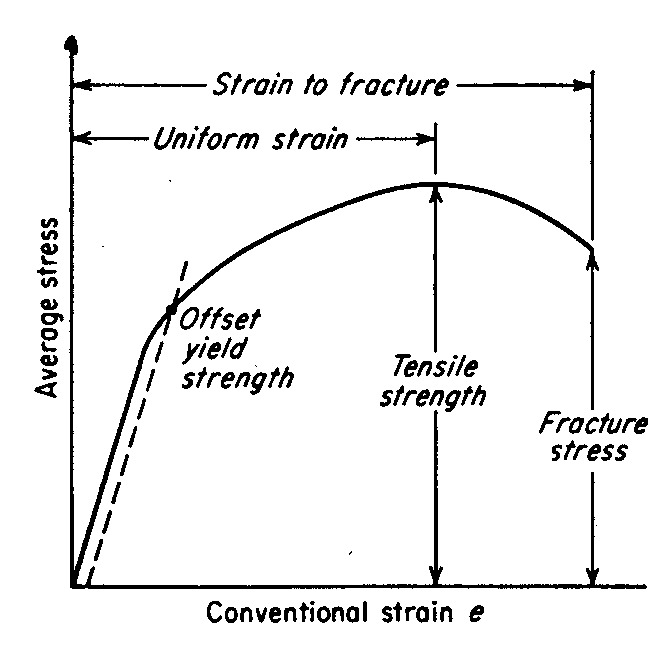
This theory is commonly referred to as the second strength theory. It posits that the primary cause of failure is the maximum linear strain of elongation. If the first principal strain reaches the limit value of uniaxial tension, regardless of the complexity or simplicity of the stress state, it results in fracture.
Failure assumption: The maximum elongation strain reaches the limit of simple tension (assuming that Hooke’s law can still be used to calculate until fracture occurs).
Failure form: Fracture
Brittle fracture conditions: ε1 = εu = σb/E;
ε1 = 1/E [σ1−μ(σ2+σ3)];
Damage conditions: σ1−μ(σ2+σ3) = σb;
Strength condition: σ1−μ(σ2+σ3)≤[σ]
Experiments have shown that this strength theory can better explain the fracture phenomenon of brittle materials such as stone and concrete under axial tension. However, it has been rarely used because its experimental results are only consistent with a few materials and it cannot widely explain the general law of brittle fracture failure.
Disadvantage: Does not explain the general law of brittle fracture failure.
Scope of application: This theory is suitable for the axial compression of stone and concrete.
This theory, known as the third strength theory, posits that the primary cause of failure is the maximum shear stress (τmax). The theory states that, regardless of the complexity or simplicity of the stress state, once the maximum shear stress reaches the ultimate shear stress value under uniaxial tension, yielding will occur.
The failure assumption is that when the maximum shear stress in a complex stress state reaches the shear stress limit of the material during simple tension and compression, failure will occur in the form of yielding. The main factor contributing to failure is the maximum shear stress, which is equal to the ultimate shear stress (τmax=τu=σs/2).
The yield failure condition is defined as τmax=1/2(σ1−σ3), and the damage conditions are met when σ1−σ3=σs. The strength condition is stated as σ1−σ3≤[σ].
Experiments have shown that this theory provides a better explanation for the plastic deformation of plastic materials. However, it should be noted that this theory does not take into account the influence of 2σ, and as a result, components designed based on this theory tend to be overly conservative.
Disadvantages: none 2 σ influence
Scope of application: suitable for general conditions of plastic materials.
The form is simple, the concept is clear, and the machinery is widely used.
But the theoretical result is safer than the actual one.
This theory is referred to as the fourth strength theory and posits that the reason for yielding in a material is the specific energy (DU) of the shape change reaching a certain limit value, regardless of the stress state.
The damage conditions are defined as 1/2(σ1−σ2)2+2(σ2−σ3)2+(σ3−σ1)2=σs, and the strength condition is given as σr4= 1/2(σ1−σ2)2+ (σ2−σ3)2 + (σ3−σ1)2≤[σ].
Experimental data from thin tube tests on several materials (steel, copper, aluminum) has shown that the shape change specific energy theory is more in line with experimental results compared to the third strength theory.
A unified form of the four strength theories can be established by having an equivalent stress (σrn) that has a unified expression of strength condition (σrn≤[σ]). The equivalent stress can be expressed as follows:
σr1=σ 1≤[σ]
σr2=σ1−μ(σ2+σ3)≤[σ]
σr3=σ1−σ3≤ [σ]
σr4= 1/2(σ1−σ2)2+(σ2−σ3)2+(σ3−σ1)2≤ [σ]
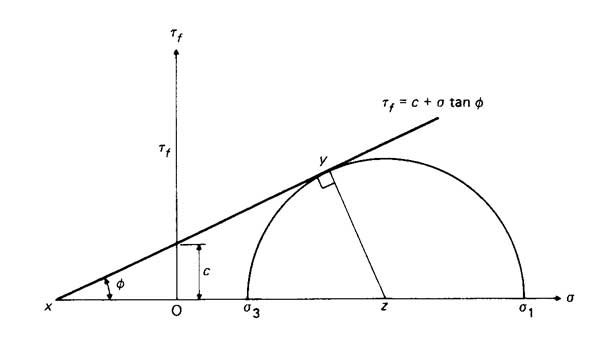
Mohr’s strength theory does not rely on the assumption that failure in materials is caused by a single factor (such as stress, strain, or specific energy) reaching its limit value. Instead, it is a strength theory that is based on the results of failure tests of materials under various stress states.
This theory considers the differences between the tensile and compressive strengths of materials, recognizes the maximum shear stress as the main cause of yielding, and takes into account the influence of normal stress on the shear plane.
While Mohr’s strength theory acknowledges the different tensile and compressive capacities of materials, which is consistent with brittle materials (such as rock and concrete), it does not account for the influence of the intermediate principal stress 2a, which is a limitation of the theory.
The strength of a material is not only determined by the nature of the material but also by the stress state at the point of failure.
Brittle materials are typically analyzed using either the strength theory of brittle fracture or Mohr’s strength theory, while plastic materials are analyzed using the strength theory of yield.
However, the mode of failure in materials is also related to the stress state. For example, under the condition of three-dimensional tensile stress, whether a material is plastic or brittle, it will fail in the form of fracture, and the maximum tensile stress theory should be used. In the case of three-dimensional compressive stress, plastic deformation occurs, and either the third or fourth strength theory should be used.
As the founder of MachineMFG, I have dedicated over a decade of my career to the metalworking industry. My extensive experience has allowed me to become an expert in the fields of sheet metal fabrication, machining, mechanical engineering, and machine tools for metals. I am constantly thinking, reading, and writing about these subjects, constantly striving to stay at the forefront of my field. Let my knowledge and expertise be an asset to your business.
EN 
DE 
ES 
FR 
IT 
NL 
PT 
RU 