Have you ever wondered why a bridge can suddenly start shaking violently or why a wine glass shatters when a singer hits a high note? This blog explores the fascinating concepts of natural frequency and resonance frequency, revealing how they impact everything from engineering marvels to everyday objects. Expect to uncover the secrets behind these vibrations and learn how they shape our world.
In daily analysis, we often confuse natural frequency and resonance frequency, and think that they are the same thing.
In fact, this is not rigorous.
Natural frequency is the performance of structural natural characteristics, while resonance frequency is the performance of structural response under external forces.
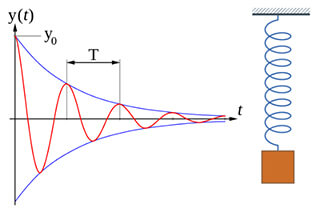
A single degree of freedom system is a system where the position can be fully determined by only one generalized coordinate at any given time. In simpler terms, the force acting on a body is in only one direction. The motion of the doll in the figure below can be represented as a spring-mass system.
A simplified model of the spring mass system can be shown in the following figure.
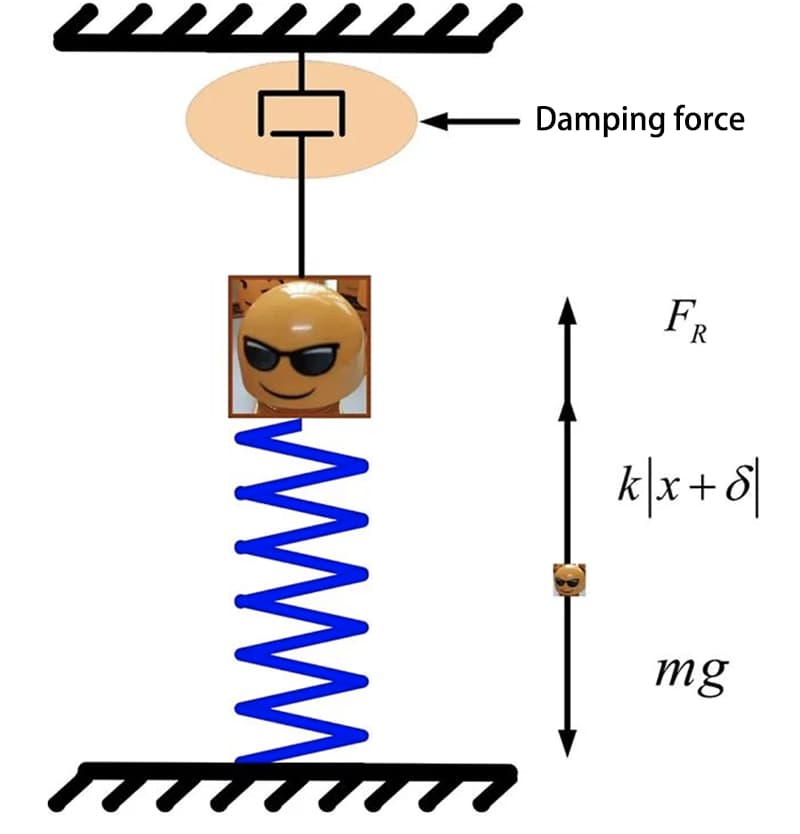
The static balance position of the pickup block is considered the coordinate origin, and it is considered positive when it moves vertically downward along the direction of spring deformation. The distance between the block and the balance position can be represented as x, and the differential equation of motion for the block can be expressed as:
Where, m is the mass of the block, k is the spring stiffness, c is the viscosity coefficient, 2n=c/m is the damping attenuation coefficient, and when the damping coefficient is zero, it corresponds to the undamped vibration system.
Natural frequency Pn:
The natural frequency is only dependent on mass and stiffness, and is not affected by factors such as damping. Structural boundary connections, material properties, shape, and other factors may impact the natural frequency, but these influences are reflected in stiffness and mass and are not the ultimate determining factors.
Free vibration is the vibration of the system without external excitation, and the motion track is related to the initial state and natural characteristics.
The forced vibration refers to the vibration generated by the system under external excitation.
The external excitation is generally a periodic or aperiodic function of time, among which the simple harmonic excitation is the simplest.
Let the simple harmonic exciting force be:
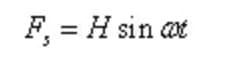
Where, H is the amplitude of exciting force, ω is the angular frequency of the exciting force.
When the block deviates from the equilibrium position by x distance, the differential equation of motion of the block is
Where, h=H/m, the above equation is the differential equation of forced vibration of single degree of freedom with viscous damping, which is a second-order constant coefficient linear non-homogeneous ordinary differential equation.
The above equation is completely consistent with the capacitive load voltage response expression we have learned in circuit theory, which is a second-order constant coefficient linear non-homogeneous ordinary differential equation.
The damping in the circuit depends on the resistance, because the resistance only consumes and does not store energy.
Under simple harmonic excitation, the total solution of the differential equation of motion of a damped system is set as:
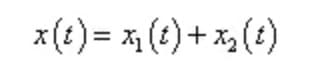
Where, x1 (t) is a homogeneous solution, which is free attenuated vibration;
Due to the existence of damping, the damped vibration part will disappear after a certain period of time.
Its solution is the same as that of free vibration, so it will not be repeated here.
Here we are concerned about the special solution x2 (t) generated by forced vibration, which can be expressed as:
Among them,
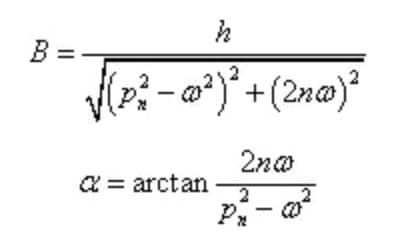
The amplitude and phase lag of the steady-state forced vibration are independent of the initial conditions, but only depend on the characteristics of the system and the excitation.
Set the frequency ratio, damping ratio and amplitude amplification coefficient as:
The above formula can be rewritten as:
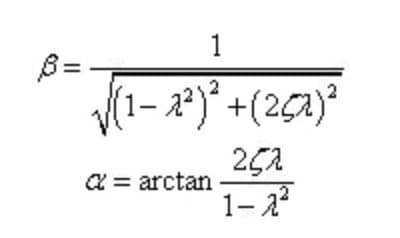
Based on this, we can know the response of the system under the forced vibration.
For better understanding, the relationship between different damping ratios, frequency ratios, and amplitude amplification coefficients can be illustrated. The frequency is separated into three regions: low-frequency, medium-frequency, and high-frequency. As seen in the figure, in both the low-frequency and high-frequency areas, the damping has a minimal impact on the amplitude amplification coefficient. Thus, the damped system can be simplified as an undamped system for easier calculation.
As mentioned above, the natural frequency is the performance of the structural characteristics of the system.
It is only related to the two factors of mass and stiffness, and has nothing to do with other factors such as damping.
There are n natural frequencies in the n degree of freedom system, and there are countless natural frequencies in the continuous system.
Resonance of a structure can lead to unpredictable behavior.
Resonance occurs at the frequency when a structure or material vibrates naturally with a large amplitude at a specific external excitation frequency.
It is the performance of excitation response according to the external excitation frequency.
The blue circle in the figure above represents the resonance frequency of the system.
When the damping of the structure is very small, the resonance frequency is approximately equal to the natural frequency of the structure;
But when the damping of the structure is large, the resonance frequency is less than the natural frequency of the structure, and the two are not consistent.
When designing the system, it is not only necessary to avoid the single frequency of the resonant peak, but also to avoid the resonant band near the resonant peak, corresponding to the intermediate frequency region in the figure above, because the response within the resonant band range is large;
It shall not be affected by the normal operation of its own equipment, but also by the structure and excitation of other equipment.
Resonance may cause collapse of lifting beam, ground resonance, machine damage and infrasonic damage, but vibration is not necessarily harmful.
For example, musical instruments can use resonance to produce sound, which has both advantages and disadvantages.
As the founder of MachineMFG, I have dedicated over a decade of my career to the metalworking industry. My extensive experience has allowed me to become an expert in the fields of sheet metal fabrication, machining, mechanical engineering, and machine tools for metals. I am constantly thinking, reading, and writing about these subjects, constantly striving to stay at the forefront of my field. Let my knowledge and expertise be an asset to your business.
EN 
DE 
ES 
FR 
IT 
NL 
PT 
RU 