Ever wondered why some materials bend easily while others remain rigid? This blog dives into the fascinating world of elastic modulus and stiffness, unraveling their crucial roles in engineering. By the end, you’ll understand how these properties influence the strength and flexibility of everyday materials.
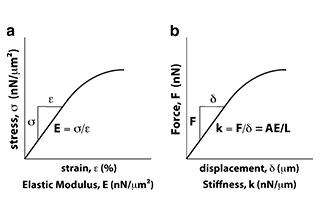
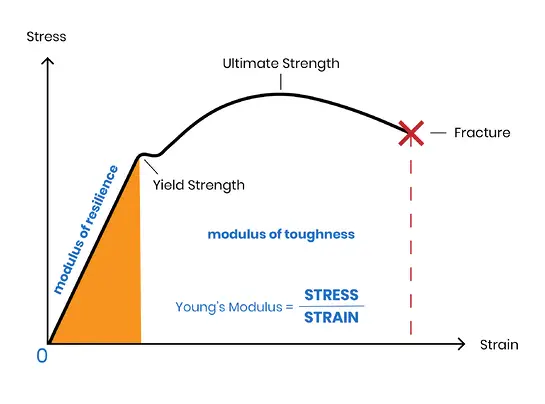
Modulus of Elasticity: The ratio of normal stress to corresponding normal strain in the elastic deformation stage of a material.
In the elastic deformation stage, a material’s stress and strain are proportional, in accordance with Hooke’s Law, and the coefficient of proportionality is referred to as the elastic modulus.
The term “modulus of elasticity” is a general description of a material’s elasticity. It encompasses several specific moduli, including Young’s modulus, shear modulus, and bulk modulus, among others.
Therefore, “elastic modulus” and “bulk modulus” are inclusive terms.
When an external force (known as “stress”) is applied to an elastomer, it will change its shape (known as “strain”). The elastic modulus is defined as the ratio of stress to strain.
For example:
Linear Strain:
When a tensile force F is applied to a thin rod, the linear stress is calculated as the tensile force divided by the cross-sectional area S of the rod.
The linear strain is calculated as the elongation of the rod (dL) divided by its original length (L).
The linear stress divided by the linear strain is equal to Young’s modulus, E = (F / S) / (dL / L).
Shear Strain:
When a lateral force (usually a friction force) f is applied to an elastomer, it changes from a square to a diamond shape.
This deformation angle is known as the “shear strain,” and the corresponding force divided by the stress area is called “shear stress.”
The shear stress divided by the shear strain is equal to the shear modulus, G = (f / S) / a.
Volume Strain:
When an overall pressure P is applied to the elastomer, it is known as “volume stress.”
The reduction in volume of the elastomer (-dV) divided by its original volume (V) is called “volume strain.”
The volume stress divided by the volume strain is equal to the bulk modulus, K = P / (-dV / V).
In general, when there is no confusion, the elastic modulus of metal materials refers to Young’s modulus, also known as the positive elastic modulus.
Unit: E (modulus of elasticity) is measured in GPa.
Elastic modulus is a crucial performance parameter of engineering materials.
From a macro perspective, it measures an object’s ability to resist elastic deformation, while from a micro viewpoint, it reflects the bonding strength between atoms, ions, or molecules.
Factors that affect bonding strength can also impact the elastic modulus of a material, such as bonding mode, crystal structure, chemical composition, microstructure, temperature, and others.
The Young’s modulus of metal materials can fluctuate by over 5% due to different alloy compositions, heat treatment states, and cold plastic deformations.
However, generally speaking, the elastic modulus of metal materials is a mechanical property index that is insensitive to structure.
Alloying, heat treatment (fiber structure), and cold plastic deformation have limited effect on the elastic modulus, and external factors such as temperature and loading rate have a negligible impact on it.
Therefore, in general engineering applications, the elastic modulus is considered a constant.
Unit: GPa (gigapascals) for elastic modulus.
The Elastic Modulus is a measure of a material’s resistance to elastic deformation.
The higher its value, the greater the stress required to produce a certain amount of elastic deformation, meaning that the material is stiffer and experiences less elastic deformation under a given stress.
The Elastic Modulus, represented by E, is a measure of the amount of stress required for a material to undergo unit elastic deformation under an external force.
It represents the material’s ability to resist elastic deformation and can be compared to the stiffness of a spring.
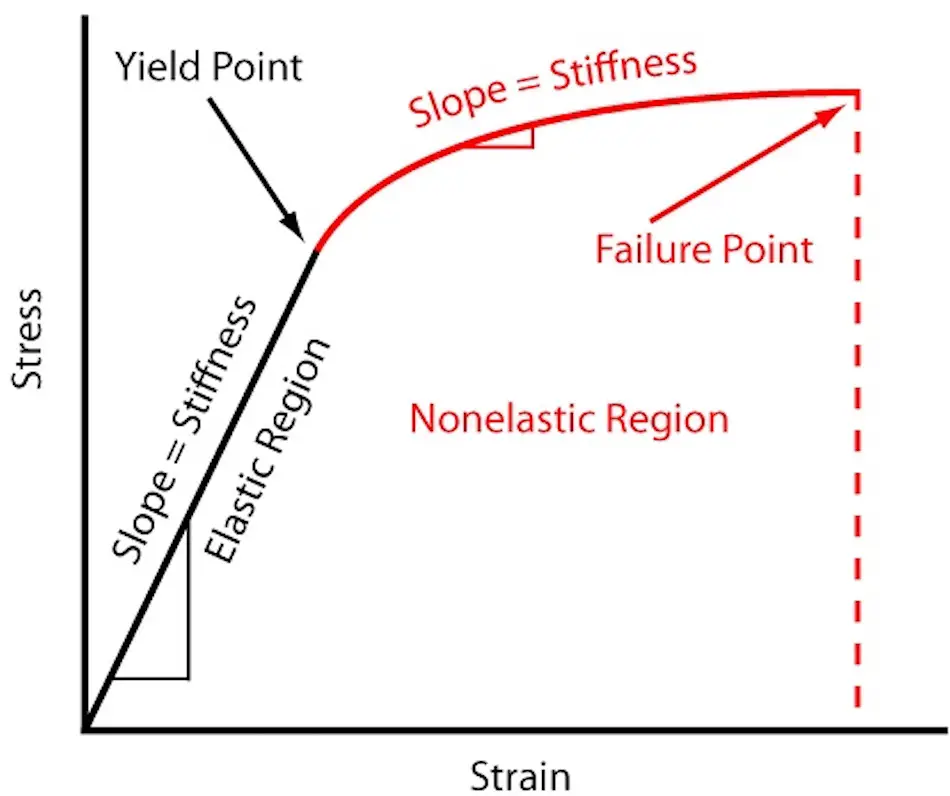
Stiffness” refers to the ability of a structure or component to resist elastic deformation. It is determined by the force or moment required to produce a unit of strain.
In terms of rotational stiffness, it is represented by “k” and can be calculated as “k = M / θ”, where “M” is the applied torque and “θ” is the rotation angle.
Other stiffnesses include:
The method of calculating stiffness can be divided into two approaches: the small displacement theory and the large displacement theory.
The large displacement theory takes into account the deformation of the structure after stress and forms the equilibrium equation accordingly, providing accurate results but with a more complex calculation process.
In contrast, the small displacement theory assumes that the structure is not significantly deformed, so the internal force can be obtained from the external load and then used to calculate the deformation.
This approach is widely used in most mechanical design applications, as it is much simpler to solve.
For example, in the calculation of beam bending deformation, the small displacement theory is often employed because the actual deformation is very small.
This theory involves ignoring the first derivative of deflection in the curvature formula and using the second derivative of deflection to approximate the curvature of the beam axis, which helps simplify the solution process by linearizing the differential equation.
When multiple loads are acting simultaneously, the bending deformation caused by each load can be calculated separately and then combined.
The resistance to deformation under a static load is known as static stiffness, while the resistance to deformation under a dynamic load is referred to as dynamic stiffness, meaning the amount of dynamic force required for unit amplitude.
When the interfering force changes slowly (i.e., the frequency of the interfering force is much less than the natural frequency of the structure), the dynamic stiffness is essentially equal to the static stiffness.
However, if the interfering force changes rapidly (i.e., the frequency of the interfering force is much greater than the natural frequency of the structure), the structural deformation will be relatively small, and thus the dynamic stiffness will be relatively large.
If the frequency of the interfering force is close to the natural frequency of the structure, resonance occurs, and the dynamic stiffness will be at its minimum, making the structure the easiest to deform, with its dynamic deformation capable of reaching several times or even more than ten times that of the static load deformation.
Excessive deformation of components can have an impact on their operation.
For instance, excessive deformation of a gear shaft can affect gear meshing, and excessive deformation of a machine tool can reduce machining accuracy.
The factors affecting stiffness include the elastic modulus of materials and the structural form. Changing the structural form can have a significant impact on stiffness.
Stiffness calculation is the foundation of vibration theory and structural stability analysis. When the mass remains constant, high stiffness results in a high natural frequency.
The stress distribution in a statically indeterminate structure is related to the stiffness ratio of each part.
In fracture mechanics analysis, the stress intensity factor of a cracked member can be determined based on its flexibility.
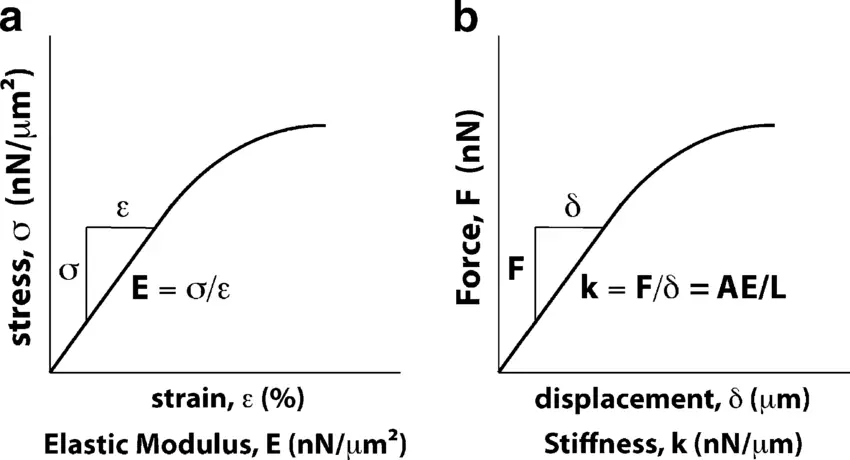
Stiffness and elastic modulus are fundamental concepts in materials science, each describing different aspects of a material’s resistance to deformation. While they are related, they serve distinct roles in the analysis and application of materials.
Elastic modulus, also known as Young’s modulus, is a specific measure of a material’s inherent ability to resist deformation under stress. It quantifies the relationship between stress (force per unit area) and strain (proportional deformation) in the linear elastic region of the material’s stress-strain curve. The elastic modulus is a material property and is independent of the material’s shape or size. It is expressed in units of pressure, such as Pascals (Pa).
Stiffness, on the other hand, is a broader term that refers to a structure’s resistance to elastic deformation under an applied load. It is not solely a material property but also depends on the geometry and boundary conditions of the structure. Stiffness is typically expressed as the force required to achieve a unit displacement (e.g., Newtons per meter, N/m).
The stiffness of a structural element can be derived from the material’s elastic modulus and the element’s geometry. For example, the flexural stiffness (EI) of a beam is the product of the elastic modulus (E) and the moment of inertia (I) of the beam’s cross-section. Similarly, torsional stiffness (GI) is the product of the shear modulus (G) and the polar moment of inertia (I).
Stiffness is crucial in engineering design, particularly for components that must maintain their shape under load, such as spindles, guide rails, and lead screws. It is also essential for structures requiring strict deformation control, such as aircraft wings and high-precision assemblies.
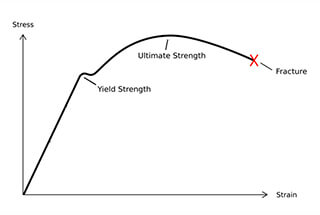
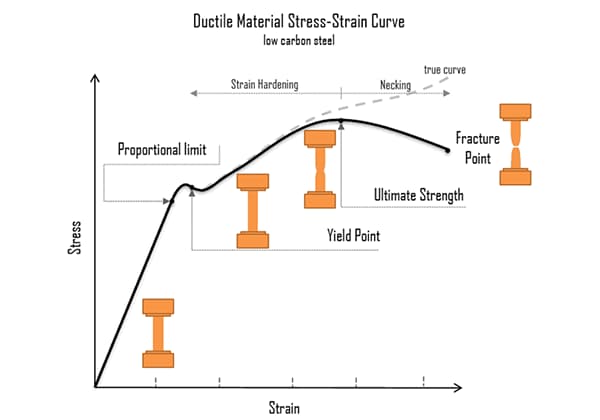
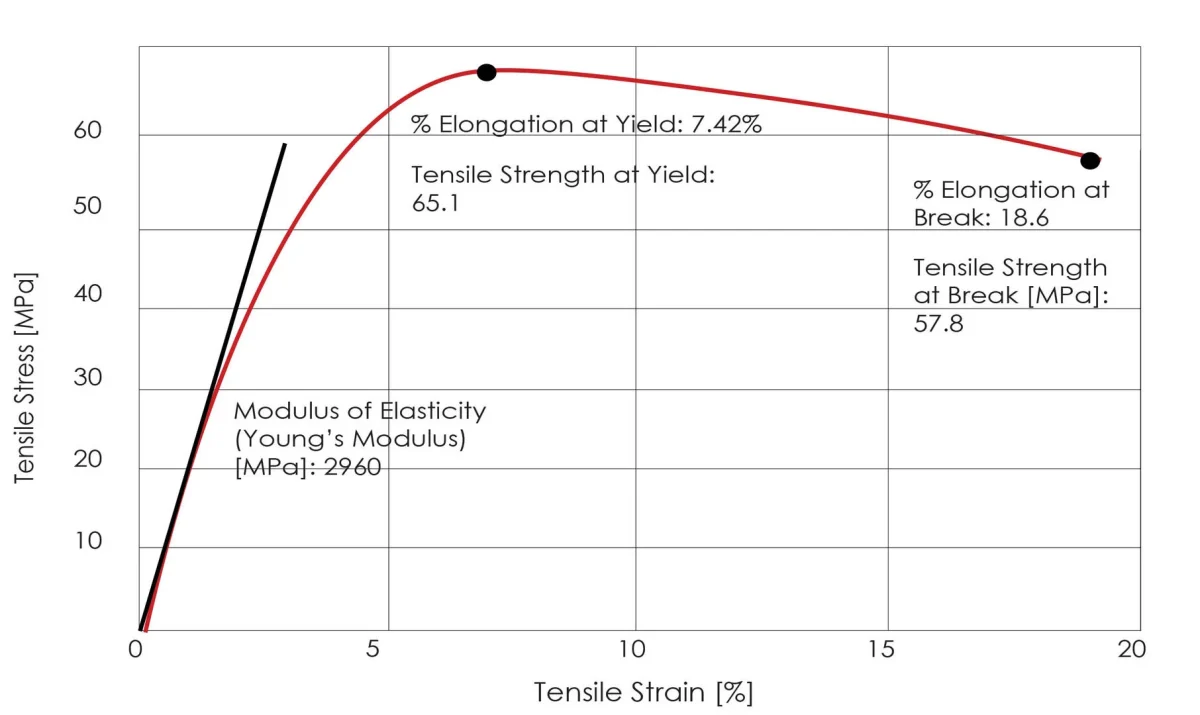
Strength is the ability of a material to resist permanent deformation and fracture under external forces. It encompasses various types of strength, including yield strength, tensile strength, compressive strength, and bending strength. These properties are critical for determining the load-bearing capacity and durability of mechanical parts.
Understanding the distinction between stiffness and elastic modulus is essential for designing and analyzing mechanical components and structures. While elastic modulus provides a measure of a material’s intrinsic resistance to deformation, stiffness considers both material properties and geometric factors to describe a structure’s overall resistance to deformation. Both concepts are integral to ensuring the performance and reliability of engineering designs.
As the founder of MachineMFG, I have dedicated over a decade of my career to the metalworking industry. My extensive experience has allowed me to become an expert in the fields of sheet metal fabrication, machining, mechanical engineering, and machine tools for metals. I am constantly thinking, reading, and writing about these subjects, constantly striving to stay at the forefront of my field. Let my knowledge and expertise be an asset to your business.
EN 
DE 
ES 
FR 
IT 
NL 
PT 
RU 