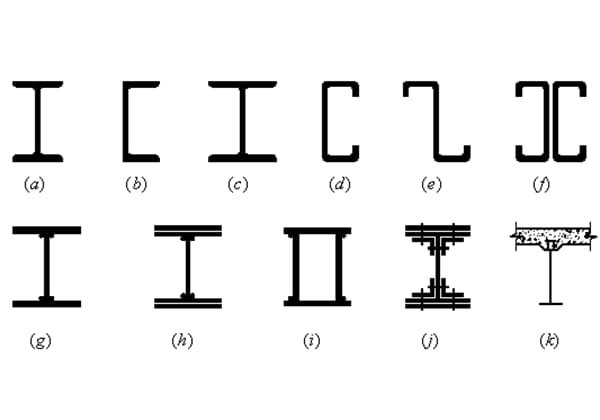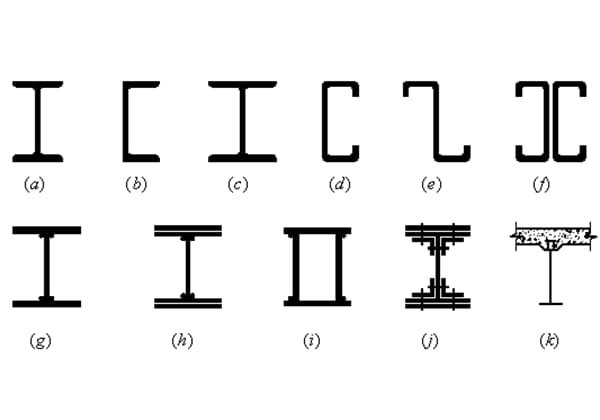
How do engineers ensure the strength and durability of beams under various loads? This article dives into the principles of bending shear stress and the conditions needed to maintain beam strength. It covers stress distribution in different beam sections—rectangular, circular, I-shaped, and thin-walled annular—while also suggesting ways to enhance beam performance through better design and material usage. Learn how shear and bending stresses interact, and discover practical tips to optimize beam construction and application.
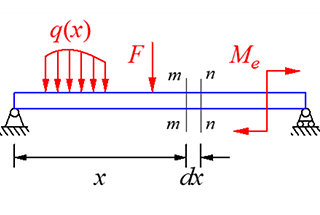
There is both bending moment and shear force on the cross-section of a beam subjected to transverse force, resulting in both normal stress and shear stress on the cross-section. The bending shear stress of several common beam sections will be discussed next.
A small segment with a length of dx is cut from the beam under transverse force bending. The beam has no load and the shear forces on both sides of the segment are equal but in opposite directions. The bending moment at the right section is greater than that at the left section, resulting in different normal stress on the two sections.
For a narrow rectangular section, the shear stress is tangent to the boundary on both sides of the beam due to the absence of shear stress on the side. This means that, as the beam is symmetrically bent and parallel to the boundary, the shear stress on the y-axis of the symmetry axis must be in the y-direction and changes little along the width direction.
Therefore, the following assumptions are made about the distribution law of shear stress on the cross section:
When the height-to-width ratio of the section is greater than 2, the solution based on the above assumption is accurate enough compared to the exact solution from elastic theory.
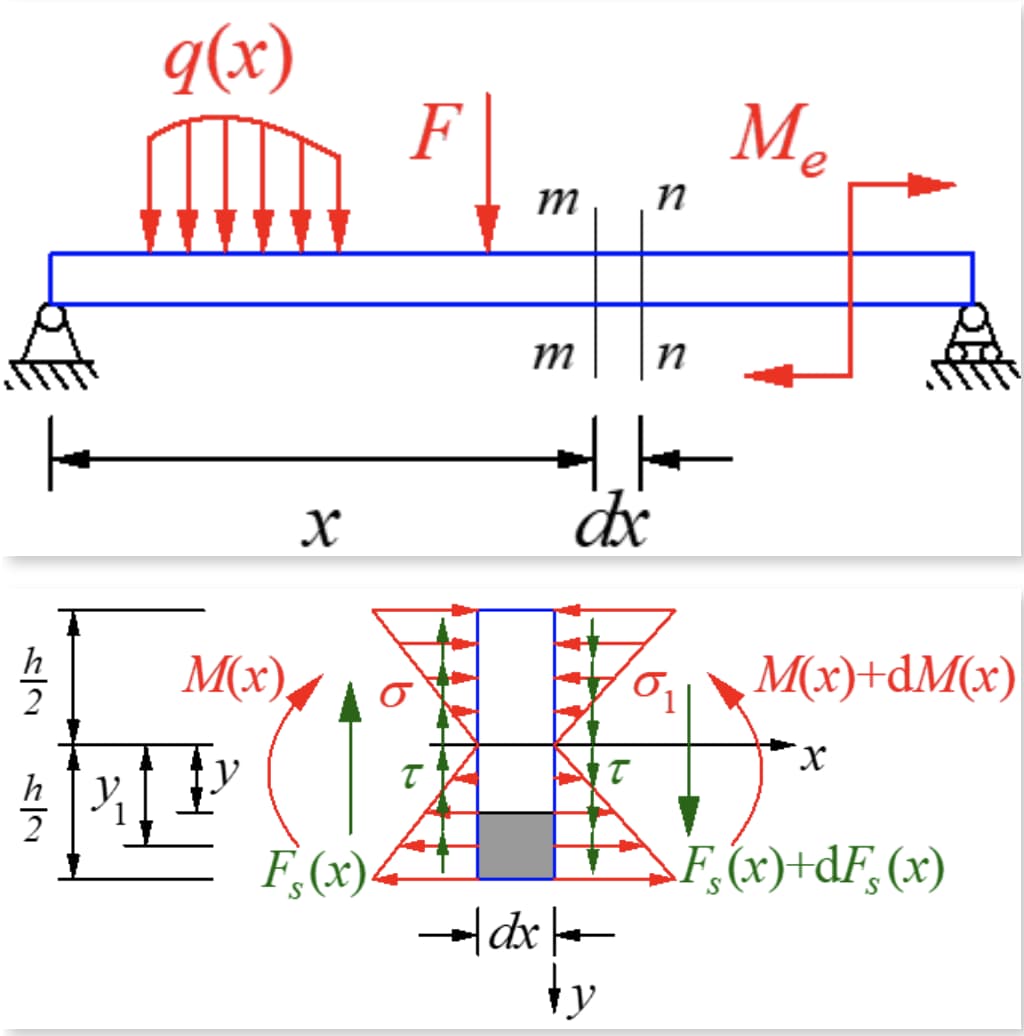
According to the shear stress reciprocity theorem, there should be a shear stress equal to the size of the cross section on the longitudinal section perpendicular to the cross section. Cut a micro segment along the longitudinal plane with the moment neutral axis away from y, and take the micro element on the lower side of the longitudinal plane. The forces are as shown in the figure below.
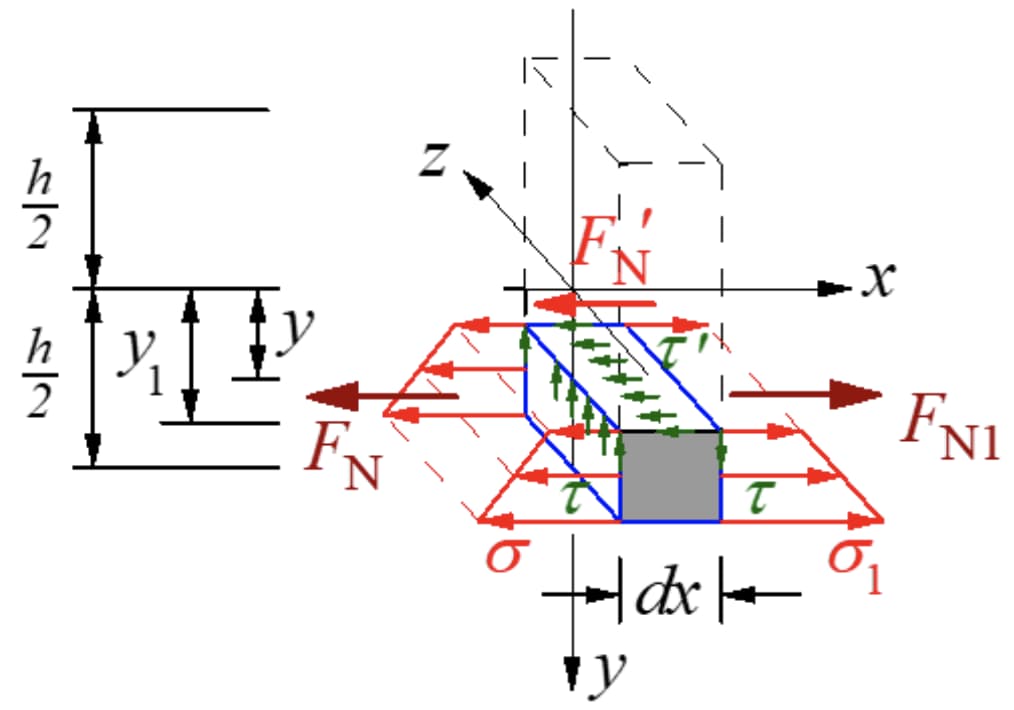
The resultant force of normal stress on the left section is:
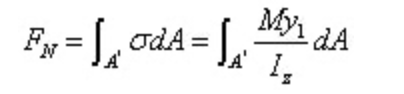
The resultant force of normal stress on the right section is：
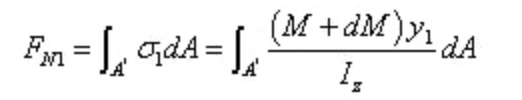
It is clear that the two resultants are of different sizes. A force along the axial direction must exist on the longitudinal section to maintain the balance of the micro segment. This force is the result of shear stress, confirming the presence of shear stress on the longitudinal section.
Since dx is a small amount, let the shear stress on the longitudinal plane be evenly distributed：
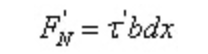
According to equilibrium conditions：
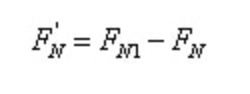
That is,
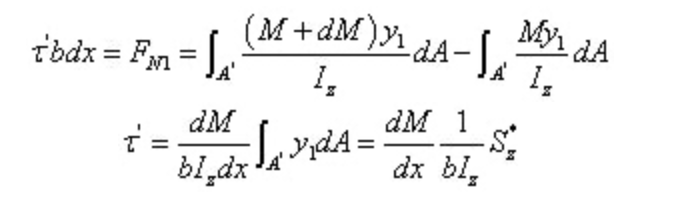
Among,
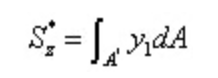
From the reciprocal theorem of shear stress and the differential relationship between shear force and bending moment:
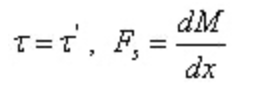
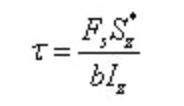
Of which:
Among,
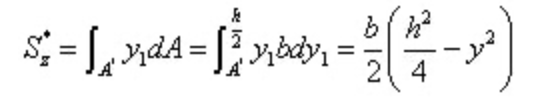
Substitute into the formula of shear stress calculation
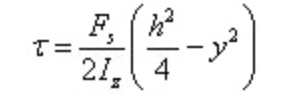
The shear stress is parabola distributed along the section height.
When y=0, there is the maximum shear stress on the section at the neutral axis
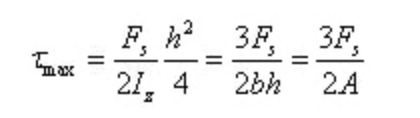
Angular strain is
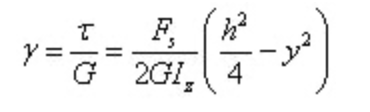
It can be seen that the angular strain is also parabola distributed along the section height.
At this time, the warping shape of the cross section when the cross force bends is shown in the figure below, which verifies that the cross force bending deformation does not meet the plane assumption.
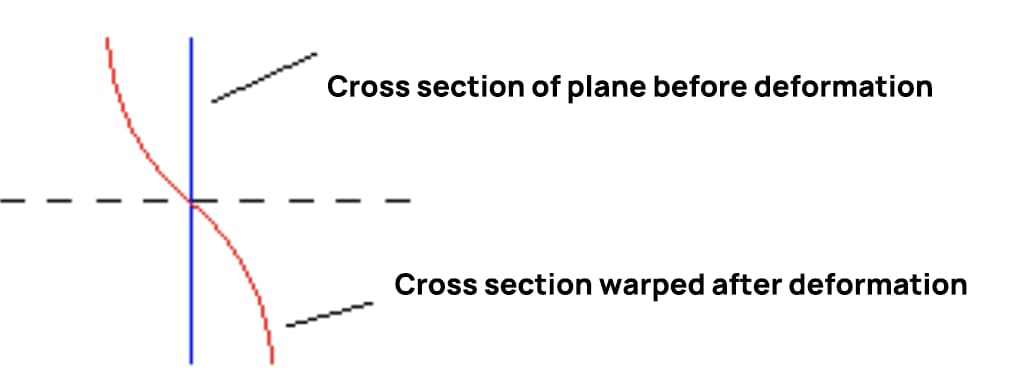
When the shear force remains constant, the shear stress on consecutive cross sections is equal, and the degree of warping is also equal. The length of the longitudinal fibers does not change due to the warping of the section, so it will not result in additional normal stress. If the shear force changes with the position of the section, the warping degree on consecutive two sections will be different, leading to additional normal stress on the section.
For symmetrical sections of other shapes, the approximate shear stress solution can be derived using the above method.
For a rectangular section, in the stress calculation formula, the section width (b) is constant, and the static moment of half the cross-sectional area on one side of the neutral axis to the neutral axis is the largest. As a result, the shear stress at each point on the neutral axis is the largest.
For symmetrical sections of other shapes, the maximum shear stress on the cross section is typically located at various points on the neutral axis, with the exception of sections with significantly increased width at the neutral axis (such as cross-sections) or some sections with variable width (such as isosceles triangle sections).
Therefore, for I-shaped, annular, and circular section beams, the maximum shear stress at each point on the neutral axis will be mainly discussed below.
The shear stress at each point on the edge of a circular section is tangent to the circumference, according to the reciprocal theorem of shear stress. At each point of the axis of symmetry, the shear stress must be in the y direction. The distribution of shear stress can be assumed to converge at a point on the axis of symmetry for each point along the width y from the neutral axis, and the components of shear stress along the Y direction at each point along the width are equal.
The maximum shear stress of the circular section is still on the neutral axis, and its direction is parallel to the external force, with the same value at each point on the neutral axis.
The maximum shear stress is
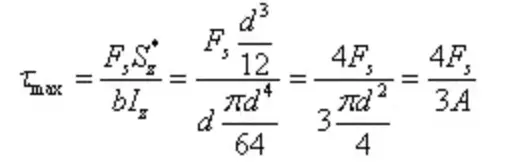
The I-shaped section is a thin-walled open section with a stress distribution as shown in the figure. The magnitude of shear stress along the wall thickness is equal, known as shear stress flow, flowing in the direction of shear.
The component of shear stress parallel to the y-axis on the flange is secondary and negligible, with the main focus on the component parallel to the long side of the flange. The shear stress on the web has a parabolic distribution, with its size shown in the figure.
The maximum shear stress is at the neutral axis.
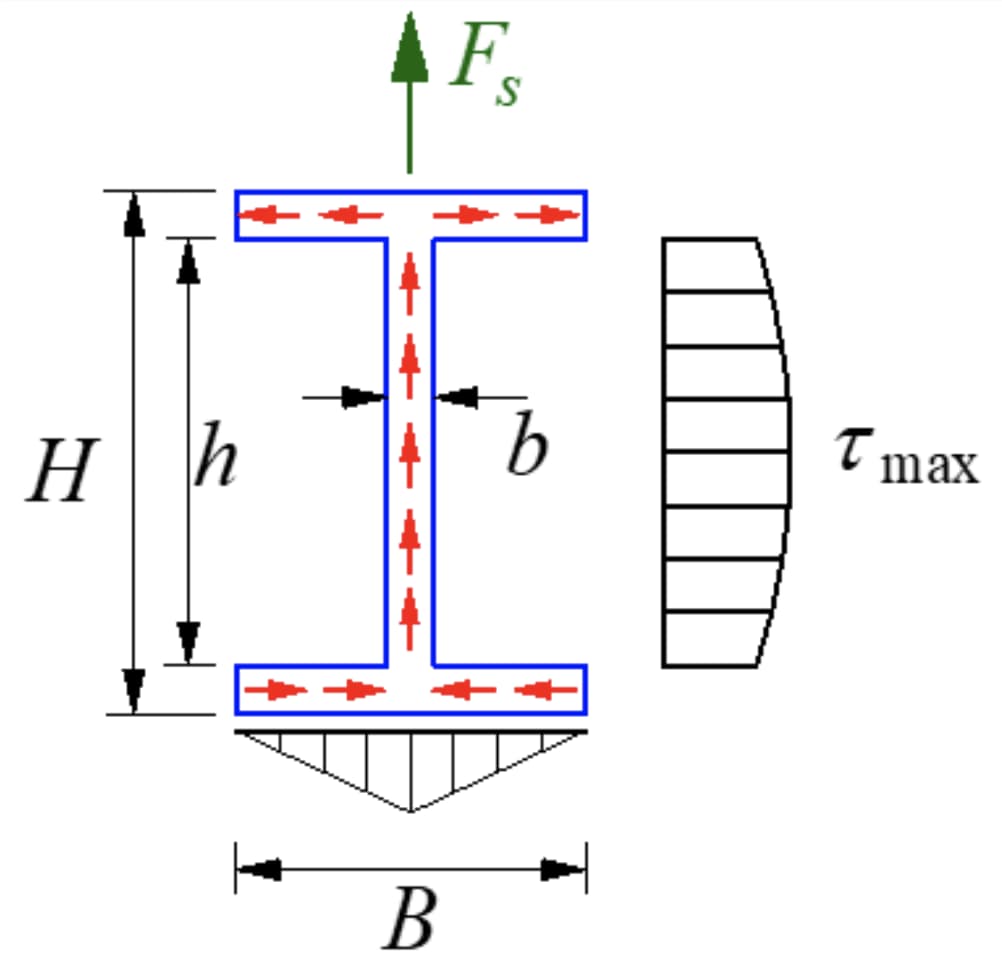
In case of I-shaped steel, the maximum shear stress:
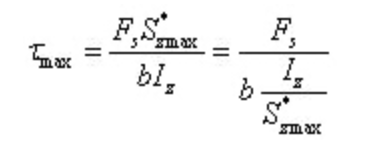
Where, b is the thickness of the web, and Iz/s*zmax can be obtained by referring to the profile steel table.
If it is an I-shaped section composed of three long and narrow rectangles, the maximum and minimum shear stresses on the web can be obtained as follows:
From the above two formulas, it can be seen that the width of the web is much smaller than the width of the flange, so the maximum shear stress on the web is not much different from the minimum shear stress.
Therefore, it can be considered that the shear stress on the web is roughly evenly distributed.
The resultant shear stress on the web accounts for 95-97% of the total shear force, and the shear force on the cross section is mostly borne by the web.
Since the web bears almost all the shear force on the section, and the shear stress on the web is nearly evenly distributed, the maximum shear stress can be approximately calculated by dividing the shear force by the cross-sectional area of the ventral pole:
At the same time, the whole area of I-beam flange is farthest from the neutral axis, and the normal stress at each point is relatively large, so the flange bears most of the bending moment on the section.
The thickness of thin-walled annular section is d, the average radius of the ring is r, and the thickness is far less than the average radius, so it can be assumed that:
The shear stress on the cross section is equal along the wall thickness;
The direction of shear stress is tangent to the central line of the section, and the direction of shear stress flow is along the shear direction.
The maximum shear stress is located on the neutral axis:
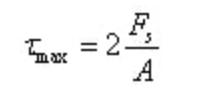
Where, A is the area of the annular section.
Bending normal stress strength condition:
For neutral axisymmetric sections, the maximum tensile normal stress and the maximum compressive normal stress are equal.
Plastic materials are commonly used, and their strength conditions:
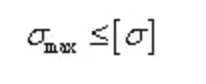
As for the section with asymmetric neutral axis, the maximum tensile normal stress and the maximum compressive normal stress are not equal.
Brittle materials are commonly used, and their strength conditions:
The strength condition of bending shear stress is:
Bending normal stress is the main factor controlling the beam.
Therefore, the strength condition of bending normal stress is often the main basis for the design of beams.
From the strength condition, to improve the bearing capacity of the beam, two aspects should be considered:
On the one hand, the stress of the beam should be reasonably arranged to reduce the maximum bending moment;
On the other hand, reasonable section shape is adopted to improve the bending section coefficient of the section and make full use of the properties of the material.
Improve the stress condition of the beam and try to reduce the maximum bending moment in the beam.
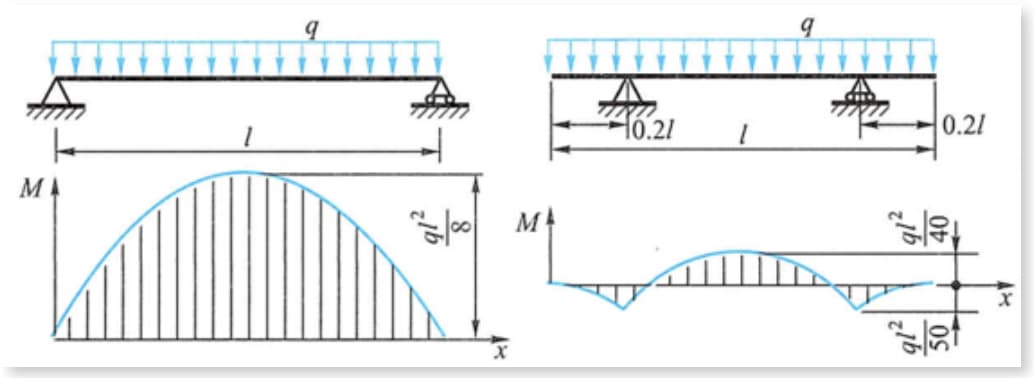
As shown in the fig., the maximum bending moment on the beam under uniform load is greatly reduced when the support is moved inward for a certain distance from the positions of both ends of the beam.
For example, the girder and cylindrical container of gantry crane, whose support point moves slightly to the middle, can achieve the effect of reducing the maximum bending moment.
The greater the flexural section coefficient, the smaller the stress and the higher the bearing capacity of the beam.
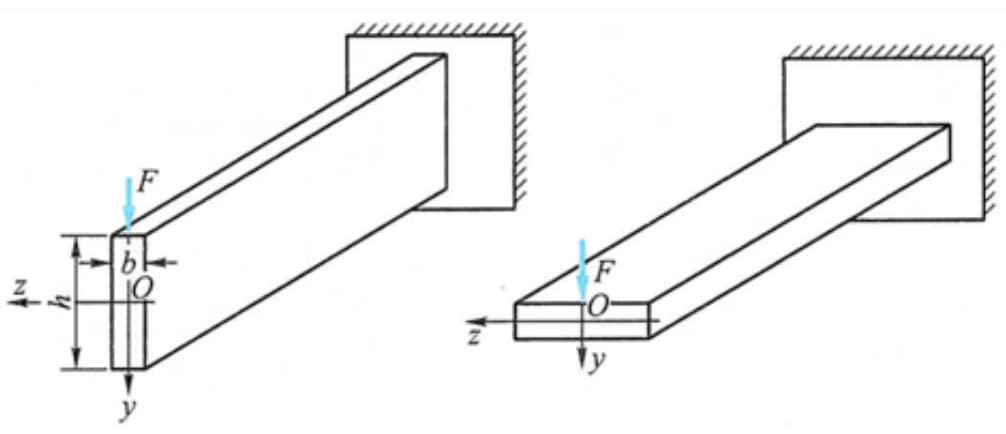
For example, when the beam is loaded in the vertical direction, the bending section coefficient is larger when the section is placed vertically, so it is more reasonable to place it vertically than horizontally.
While improving the bending section coefficient of the section, we also hope to use less materials to achieve better economy.
Therefore, the ratio of bending section coefficient to section area is generally used to measure the rationality of section design.
Under the same cross-sectional area, rectangular section (height greater than width) is more reasonable than circular section, while I-shaped section or box section is more reasonable than rectangular section.
Therefore, in order to make full use of materials, materials should be placed as far away from the neutral axis as possible.
When discussing the reasonable shape of the section, the mechanical properties of the material should also be taken into account.
Materials with the same tensile and compressive strength (such as low carbon steel) should adopt neutral axisymmetric sections, such as circular, rectangular, I-shaped, box, etc.
In this way, the maximum tensile stress and the maximum compressive stress at the upper and lower edges of the section can be equal.
For materials with unequal tensile and compressive strengths (such as cast iron, cement, etc.), the section shape with the neutral axis inclined to the tensile side should be adopted.
The beams discussed above are all of equal section, and the bending section coefficient is constant, but generally, the bending moment of each section of the beam changes with the position of the section.
The section design of equal straight beam should be carried out according to the maximum bending moment, and its maximum stress is close to the allowable stress.
The bending moment on other sections is small, so the stress is small, and the material is not fully utilized.
In order to save materials and reduce self weight, the section size can be changed so that the bending section coefficient changes with the bending moment.
A larger section is used where the bending moment is larger, while a smaller section is used where the bending moment is smaller.
This kind of beam whose section changes along the axis is called variable section beam.
If the maximum normal stress on each cross-section of a variable cross-section beam is equal and equal to the allowable stress, it is called an equal strength beam.
As the founder of MachineMFG, I have dedicated over a decade of my career to the metalworking industry. My extensive experience has allowed me to become an expert in the fields of sheet metal fabrication, machining, mechanical engineering, and machine tools for metals. I am constantly thinking, reading, and writing about these subjects, constantly striving to stay at the forefront of my field. Let my knowledge and expertise be an asset to your business.
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO