Ever wondered how engineers accurately determine the unfolded size of sheet metal? This process is crucial in manufacturing to ensure precise dimensions after bending. This article breaks down two main methods: the bending compensation and bend deduction algorithms. By understanding these techniques, you’ll gain insights into the science behind sheet metal fabrication and improve your design accuracy. Dive in to discover how you can master the art of calculating sheet metal unfold sizes efficiently.
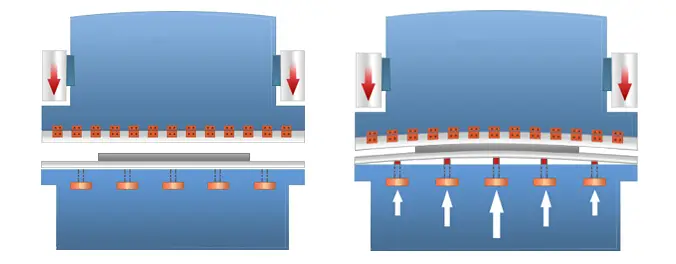
For sheet metal bending and expansion, one side of the sheet will be elongated while the other side will be compressed. The factors that affect this process include the type of material, its thickness, heat treatment, and the bending angle.
To ensure the desired size of parts after the final bending process using a press brake, the design of sheet metal parts utilizes various algorithms to calculate the actual length of the sheet metal under the folding condition. One of the most widely used methods is the simple “pinch rule,” which is based on personal experience in the calculation.
However, with the advent and widespread use of computer technology, more people are turning to computer-aided design methods. In general, there are two popular algorithms for sheet metal bending that are widely adopted today. The first is based on the bending compensation algorithm, and the second is based on the bending deduction algorithm.
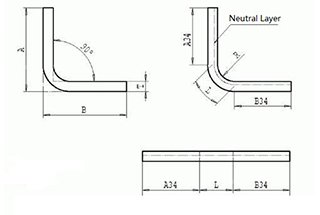
The bending compensation algorithm calculates the expansion length (LT) of a part by adding the length of each section of the part after flattening and the length of the flattened bend area, which is referred to as the “bend compensation” value (BA). The formula for the length of the entire part is as follows: LT = D1 + D2 + BA.
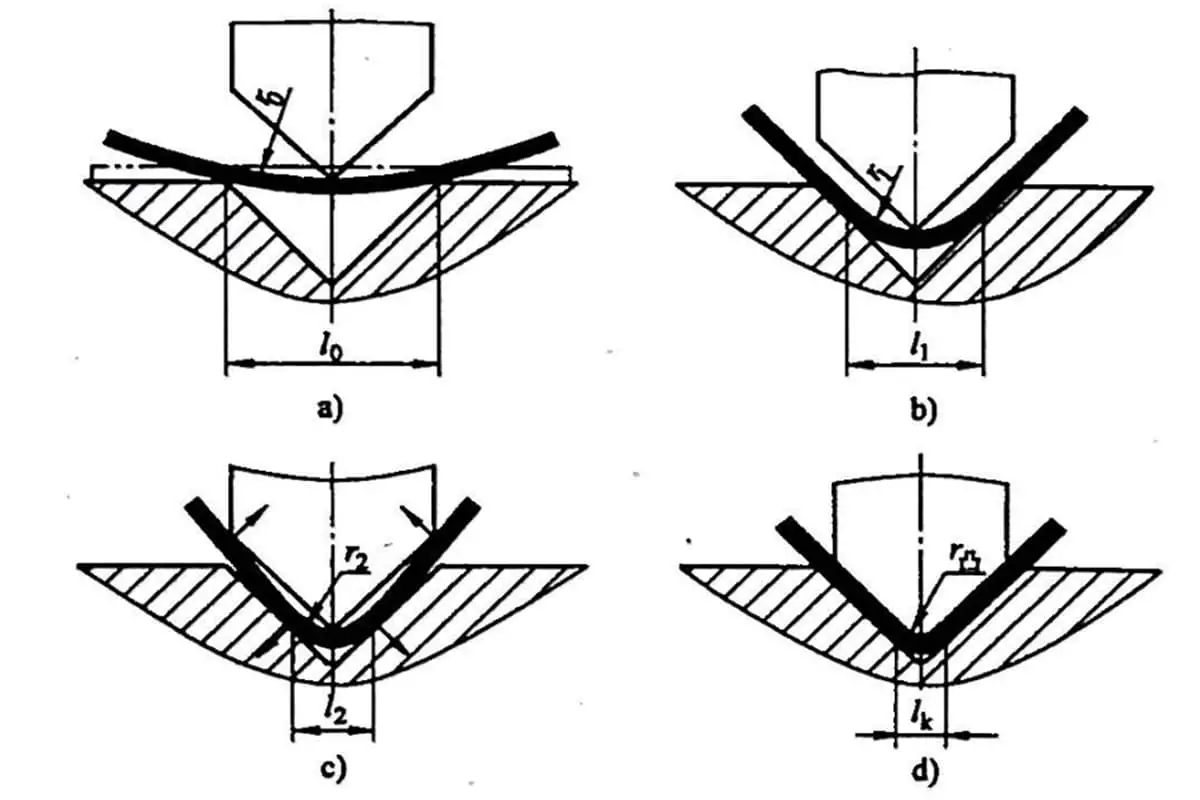
The bending area is assumed to deform during the bending process. To determine the geometry of the unfolded parts, the following steps should be taken:
Bend deduction refers to the amount of reverse bend and is a simple algorithm used to describe the sheet metal bending process.
According to this method, the flattening length (LT) of the part is equal to the sum of the length of the two theoretical flat sections extending to the “sharp point” (the imaginary intersection of the two flat sections) minus the bend deduction (BD) value.
Expand Calculation Principle:
When the bending radius is large and the bending angle is small, the degree of deformation is minimal, and the neutral layer is close to the center of the sheet’s thickness.
Conversely, when the bending radius decreases and the bending angle increases, the degree of deformation increases, and the position of the neutral layer gradually moves towards the inner part of the bending center.
The distance from the neutral layer to the inside of the sheet is represented by λ.
Basic Formula for Expansion Calculation:
Expansion length = inner layer + inner layer + compensation amount
As the founder of MachineMFG, I have dedicated over a decade of my career to the metalworking industry. My extensive experience has allowed me to become an expert in the fields of sheet metal fabrication, machining, mechanical engineering, and machine tools for metals. I am constantly thinking, reading, and writing about these subjects, constantly striving to stay at the forefront of my field. Let my knowledge and expertise be an asset to your business.
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO