Analyzing Sheet Metal Bending Process Parameters

To enhance the precision of bending elevator sheet metal components, the bending radius (R-angle) of commonly used materials such as SPC, SPHC, SUS304, and 804-GG was accurately measured at a 90° angle using a CNC press brake in the sheet metal workshop. An optical measuring instrument was utilized to determine the bending radius, and the bending coefficient was calculated with the aid of vernier calipers.

The test results serve as a reference and provide data support for selecting appropriate bending tooling, enhancing the accuracy of the R-angle during bending, and improving the accuracy of calculating bending dimensions.

Test Significance

The bending radius (inside R) and bending coefficient are crucial factors that impact the quality of the bending process. The bending radius is associated with the bending tool, material thickness, and performance factors, while the bending coefficient is determined by the material thickness, bending radius, and bending angle. The bending coefficient also affects the unfolded dimensions of the workpiece.

The current formula for calculating the 90° bending factor is α = 1.36t + 0.43R (where t represents the material plate thickness). Some of the common errors in calculating the bending factor include:

• The difference between the t value and the actual thickness of the material.
• The deviation between the actual bending inside R and the required inside R as indicated in the drawing (inside R is usually taken from the drawing when calculating α).
• The use of R gauge measurement (where R gauge values below R3 are 0.25 and above R3 are 0.5) in determining the bending R, which results in lower accuracy.
• The influence of the material and bending method on the bending R is not taken into account.

When a workpiece is bent multiple times, the error in the bending coefficient accumulates, leading to poor dimensional accuracy in the finished product.

To address these issues, this experiment measured the actual thickness of several bending materials, utilized an optical measuring instrument to more accurately determine the inside and outside bending radius, calculated the actual bending coefficient of the workpiece, and compared the results with the formula. This will aid in the selection of appropriate bending dies, improve the accuracy of the bending forming R, and expand the accuracy of dimensional calculations.

Test scheme

Test material

The test materials used in the experiment were SPCC, SPHC, SUS304, and 804-GG, which were purchased by our company. The thickness specifications for each material can be found in Table 1.

Table 1 Test materials and thickness (mm)

Test specimen

The size of the samples used in the experiment was 100mm x 100mm and they were produced using laser cutting and blanking. This ensured that the dimensional accuracy of the samples was at a level of 0.1mm.

Test equipment

The test bending machine used in the experiment was a CNC press brake located in the elevator production sheet metal workshop. The V-groove used in the experiment featured both FASTI-50 and Beyeler, and the scimitar upper die was selected, as depicted in Figure 1.

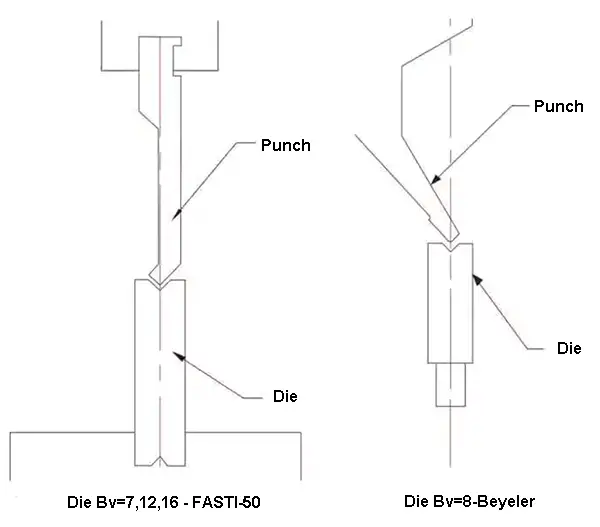
Fig.1 V-groove bending die

The three-point bending machine used in the experiment was a 3P250. The straight knife upper die selected for the experiment included both the pointed cutter R7 and the round cutter R9, as illustrated in Figure 2.

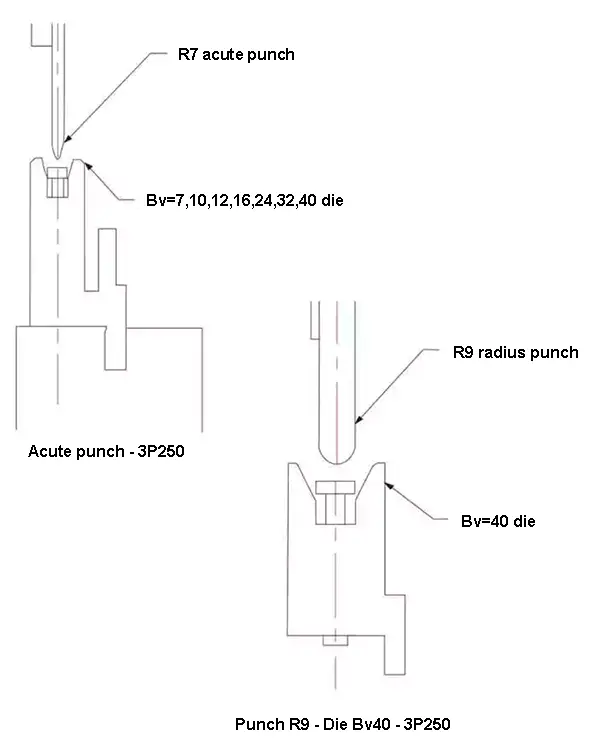
Fig.2 Three-point bending die

Table 2 The parameters of press brake, punch & die

Test method

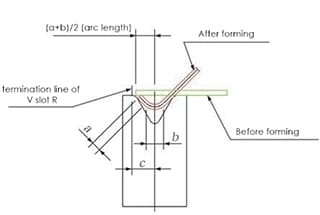
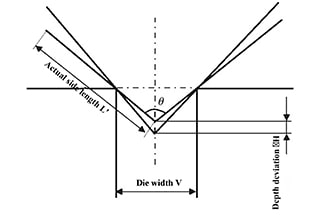
The true thickness of the specimens was measured using a micrometer, and four pieces were averaged for each specific thickness. The specimens were bent using different bending dies at a bending angle of (90 ± 1)°, with the goal of ensuring that one side of the specimens had a length of 50mm, as depicted in Figure 3.

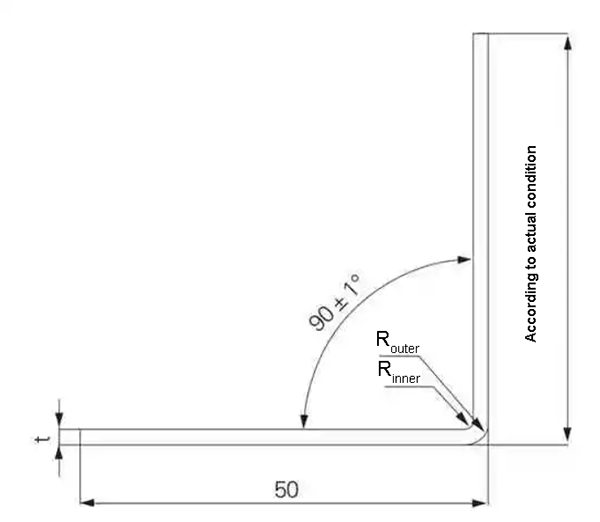
Figure 3 Test Bending Diagram

Each thickness specification was repeated 5 times during the bending process. After the bending was finished, the bending angle contours were scanned using an optical measuring instrument to calculate the outer bending angle (R outside) and inner bending angle (R inside), as illustrated in Figure 4.

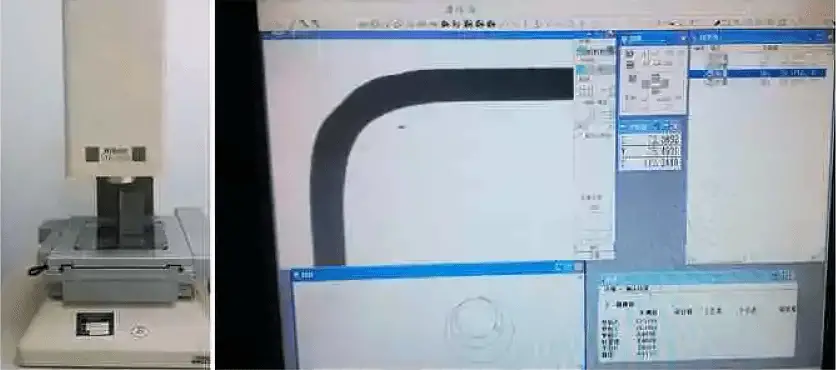
Fig. 4 Optical measuring instrument and bending R-angle measurement

A vernier caliper was used to measure the length of both sides in order to calculate the bending coefficient. Each thickness specification was repeated 5 times, and the average value was taken.

Test results and analysis

The attached table is a compilation of the test results. The data displayed in the table includes the actual thickness of the test material, the inner and outer radius of the 90° bend, the bending coefficient, and the thinning of the bend.

Actual material thickness

Table 3 compares the actual thickness of the specimen, as measured with a micrometer, with its nominal thickness.

Table 3 The actual thickness of the test materials (mm)

The table reveals that the difference between the actual thickness of SPCC and its nominal thickness is within 0.03mm. The actual thickness of the uncoated SUS304 material was found to be about 0.07mm thinner than its nominal thickness. The actual thickness of the 4.5mm hot rolled plate SPHC was measured at 4.2mm.

Bending inside angle R_inner

Comparing the R_inner under different bending conditions, it can be seen that the R_inner is influenced by the material, plate thickness, bending method, and bending tooling.

Of these four factors, the situation of three other factors being equal:

• R_inner(SUS304) > R_inner (SPCC).

If the width of the V-groove Bv = 12 mm, the R_inner in SPCC with the thickness of 1.2 mm and SUS304 is 1.85 mm and 2.09 mm, respectively.

• When the bending die is the same, for the same material, the plate thickness of R_innerinfluence is less.

For example, when Bv = 12mm in three-point bending, R_inner in 1.0 ~ 2.0mm thickness of SUS304 is 2.33 ~ 2.51mm, the difference is not significant.

• R_inner(three-point) > R_inner (V-groove).

Comparing the same slot width bending lower die (Bv=7mm, 12mm and 16mm) shows that the bending R_inner in three-point is slightly larger than that in V-groove.

• The larger the slot width Bv, the larger the R_inner, and the larger the corresponding R_inner

Figure 5 is a comparison of the three-point bending R angles for the lower die slot width Bv is 24mm, 32mm and 40mm, corresponding to about 4.0mm, 4.7mm and 5.9mm of R_inner, respectively.

Fig. 5 Comparison of the inside radius of 4.5 mm SPHC bending with different slot widths (three-point acute punch)

Therefore, in addition to the bending die slot width Bv, the material, bending method (V-slot and three-point) also affects the bending R_inner, which should be paid attention to.

Reducing ratio and outside bending angle R_outer

In the test, the difference between R_outer and R_inner is used to represent the average thickness near the bending angle, i.e., t’ = R_outer – R_inner.

Thus, reducing ratio is η = (t – t’)/t.

From the data in the attached table, it can be seen that thickness reduction occurred in all cases in this test case.

Most of the reducing ratio is within 6%-15%, and the influence of material thickness, bending mode and slot width on the thinning rate is more complicated, and the rule is difficult to identify.

However, it can be seen that the SPHC thinning rate is lower, about 4% to 6%.

The test’s R_inner uses an optical measuring instrument to scanning calculate, while the roundness value can be calculated.

(1) When Bv = 7 ~ 16mm, the roundness value of R_inner and R_outer is very small, most of which is ≤ 0.05mm, indicating that the bent inner and outer corner contours highly match the degree of roundness.

(2) When Bv = 24mm, 32mm and 40mm (all three-points type), the roundness values of R_inner and R_outer are slightly increased, exceeding 0.1mm, which means that after the groove width Bv of the lower bending dies increases to 24mm, the degree of arc of the inner and outer contours of the bending decreases.

Bending coefficient α

The schedule also gives the measured and calculated values of the bending coefficient test (currently method used to calculate the bending coefficient, calculation formula: α = 1.36t + 0.43R_inner).

For comparison, the difference is not large (in the calculation, the thickness t and R_inner are both brought into the calculation by the actual test value), which indicates that the current bending coefficient formula α = 1.36t + 0.43R_inner is universal, the bending coefficient depends on two parameters in the actual thickness t of the material and the actual bending R_inner.

The R_inner is influenced by the material, plate thickness, bending method and bending tool, the actual R_inner is the simplest and most effective method.

For new materials or bent parts with other thicknesses, it is necessary to actually measure the true thickness and the bending R_inner of the bending tool.

Conclusion

Based on the above analysis, several conclusions can be obtained:

(1) The test results show the bending R_inner, R_outer and bending coefficients of several commonly used thickness sheet of SPCC, SPHC, SUS304, 804-GG in the sheet metal workshop CNC press brake machines like Beyeler, FASTI-50 and 3P250;

(2) R_inner is not only related to the bending die but also related to the material;

The test shows that the R_inner of SUS304 is slightly larger than that of SPCC under the same bending parameters;

(3) When the other bending parameters are the same, the R_inner of the three-point bending is slightly larger than the V-groove bending, so the bending work center should be considered when selecting the bending coefficient;

(4) The bending coefficient calculation formula α=1.36t+0.43R_inneris universal.

Accumulating the real thickness of the commonly used bending materials in the workshop and the corresponding bending mold forming R_inner can calculate a more accurate bending coefficient.